1-AVirtualSpaceTimeTravelMachine.Ang
1713 reference(s) | 2-demo_14
176 reference(s) |
3-xiirf_____.nota.t.
151 reference(s) | 4-Web_Mail.01.vv
137 reference(s) |
5-xiirv_____.nota.t.
124 reference(s) | 6-EnsembleDesGaleries.DIAPO.0978
122 reference(s) |
7-Stereogrammes_AutoStereogrammes.01
105 reference(s) | 8-Fractal.01
93 reference(s) |
9-UlamSpiral.01.Fra
86 reference(s) | 10-Galerie_NumberTheory.FV
84 reference(s) |
11-catalogue.11
82 reference(s) | 12-Fractal.21
79 reference(s) |
13-ChatGPT.01.Fra
79 reference(s) | 14-BEST.20070728
75 reference(s) |
15-Vcatalogue.11
72 reference(s) | 16-An2000.01.Fra
72 reference(s) |
17-mail.01.vv
71 reference(s) | 18-Galerie_Pi.FV
69 reference(s) |
19-ImagesDuVirtuel.01.Fra.FV
68 reference(s) | 20-Fractal.11
68 reference(s) |
21-help.
66 reference(s) | 22-xciP_____interpole.01.z.
65 reference(s) |
23-DecimalesDePi.01.Fra
65 reference(s) | 24-xiirs_____.nota.t.
62 reference(s) |
25-LOG_xiMc.11
62 reference(s) | 26-EnsembleDesGaleries.DIAPO.0001
62 reference(s) |
27-NombresPremiers_10000.vv
61 reference(s) | 28-IAGenerativesImages.01.Fra
58 reference(s) |
29-AProposSite.01.Fra
58 reference(s) | 30-NombresEtLumiere.01.vv.Fra
57 reference(s) |
31-Galerie_ArtisticCreation.FV
57 reference(s) | 32-Pcatalogue.11
56 reference(s) |
33-ExpV_VirE.11
56 reference(s) | 34-EntrelacsIntertwinings.01.Fra
56 reference(s) |
35-De_L_EnseignementAssisteParOrdinateur_a_L_ExperimentationVirtuelle.01.Fra
55 reference(s) | 36-Polynomials_RationalNumbers.01.Fra
54 reference(s) |
37-Multivers.01.Fra
54 reference(s) | 38-Galerie_ImagesDesMathematiques.FV
54 reference(s) |
39-FloatingPointNumbers.01.Fra
54 reference(s) | 40-EnsembleDesGaleries.DIAPO.0979
53 reference(s) |
41-AVirtualSpaceTimeTravelMachine.Fra
53 reference(s) | 42-PatrimoineHumanite.02.Fra
52 reference(s) |
43-MouvementsRelatifs_et_ObservationsAstronomiques.01.Fra
52 reference(s) | 44-FloatingPointNumbers.01.Ang
52 reference(s) |
45-Exposition_EcolePolytechnique_FeteDeLaScience_201910
52 reference(s) | 46-copyright.01.
51 reference(s) |
47-PerteDeLAssociativite.01
51 reference(s) | 48-Informations_GoodNewsAndBadNews.01.Ang
51 reference(s) |
49-Galerie_NewPictures.FV
51 reference(s) | 50-Informations_AboutPicturesAnimationsAndFiles.01.Ang
50 reference(s) |
51-Galerie_Tributes.FV
49 reference(s) | 52-SurfaceProjector.01.Ang
48 reference(s) |
53-GoldenTriangle.01.Fra
48 reference(s) | 54-Galerie_ArtAndScience.FV
48 reference(s) |
55-Kepler.02.
47 reference(s) | 56-EnsembleDesGaleries.DIAPO.0590
47 reference(s) |
57-ConjectureDeSyracuse_0128.Parity.vv
47 reference(s) | 58-xiia_____.nota.t.
46 reference(s) |
59-Bard.01.Ang
46 reference(s) | 60-IAGenerativesImages.01.Ang
45 reference(s) |
61-Informations_GoodNewsAndBadNews.01.Fra
44 reference(s) | 62-GoldenTriangle.01.Ang
44 reference(s) |
63-FaireDesMathematiques.01.Fra
44 reference(s) | 64-LesCourbesRemplissantes.02.Fra
43 reference(s) |
65-LeParadoxeDeFermi.01.Ang
43 reference(s) | 66-Galerie_NonDeterministicFractalGeometryNaturalPhenomenonSynthesis.FV
43 reference(s) |
67-Fractal.02
43 reference(s) | 68-DieuScience.01.Fra
43 reference(s) |
69-Fractal.03
42 reference(s) | 70-ExpV_VirE.Ang
42 reference(s) |
71-xrs_____CalabiYau.22.K.
41 reference(s) | 72-MonodimensionalCellularAutomata.01.Fra
41 reference(s) |
73-LeNoeudInfini.01.Fra
41 reference(s) | 74-Galerie_ImagesEssentiellesDesMathematiques.FV
41 reference(s) |
75-Galerie_ImagesDidactiques.FV
41 reference(s) | 76-Exposition_EcolePolytechnique_NuitDesChercheurs_201309
41 reference(s) |
77-NombresEtLumiere.02.vv.Ang
40 reference(s) | 78-Galerie_NumbersAndLight.FV
40 reference(s) |
79-Exposition_MairieCinquiemeArrondissementParis_202001_202002
40 reference(s) | 80-DieuScience.01.Ang
40 reference(s) |
81-DecimalesPi_1_100.vv
40 reference(s) | 82-xrs_____CalabiYau.87.I.
39 reference(s) |
83-xcg_____z_COHX.01.K.
39 reference(s) | 84-VisitesGaleriesEnfouies.01.Ang
39 reference(s) |
85-MathematiquesPhysiqueFractales.02
39 reference(s) | 86-DuModeleALImage.02.Fra
39 reference(s) |
87-AnimFractal.01.
39 reference(s) | 88-xrq_____particle.M5.I.
38 reference(s) |
89-FaireConnaitre_FaireAimer_LesMathematiques.01.Fra
38 reference(s) | 90-DecimalesPi_100000.vv
38 reference(s) |
91-Notations_AppartientA.01
37 reference(s) | 92-xiirk_____.nota.t.
36 reference(s) |
93-xciP_____luminance.01.z.
36 reference(s) | 94-OrdinateursEtCalculs.01.Fra
36 reference(s) |
95-LesCourbesRemplissantes.01.Ang
36 reference(s) | 96-GenieLogiciel.01.Fra
36 reference(s) |
97-Commentaires_NKleinBottle.01
36 reference(s) | 98-xrs_____cylindre.21.I.
35 reference(s) |
99-xiird_____.AC2B.3.11..u.
35 reference(s) | 100-RealNumbers.01.Fra
35 reference(s) |
101-ChatGPT.01.Ang
35 reference(s) | 102-ArtScience.01
35 reference(s) |
103-xrk_____SinCos.11.K.
34 reference(s) | 104-xivP_d09_f2_____.REFL.E.12.2..u.
34 reference(s) |
105-relai_universel.01.vv
34 reference(s) | 106-fractal.01
34 reference(s) |
107-Polynomials_RationalNumbers.01.Ang
34 reference(s) | 108-NatureDesMathematiques.01.vv.Fra
34 reference(s) |
109-MesExpositionsPassees.01
34 reference(s) | 110-ImpossibleStructures.01.Ang
34 reference(s) |
111-EnsembleDesGaleries.DIAPO.0954
34 reference(s) | 112-EnsembleDesGaleries.DIAPO.0591
34 reference(s) |
113-Autostereograms.01.
34 reference(s) | 114-xrs_____sphere.19.I.
33 reference(s) |
115-xrs_____bKlein.14.I.
33 reference(s) | 116-xrs_____CalabiYau.42.K.
33 reference(s) |
117-xrc_____tric_cos.81.K.
33 reference(s) | 118-xci_____o_carre.81.K.
33 reference(s) |
119-xDarchivesG__CMS5__sources__CMS5_____SIS_CMS5_1
33 reference(s) | 120-real.01.vv.
33 reference(s) |
121-VirtualChaos.01.Fra
33 reference(s) | 122-VirtualChaos.01.Ang
33 reference(s) |
123-SurfaceProjector.01.Fra
33 reference(s) | 124-RasoirDOccamEtMathematiques.01.vv.Fra
33 reference(s) |
125-NDimensionalDeterministicFractalSets.01.Fra
33 reference(s) | 126-MorePages.Ang.
33 reference(s) |
127-MartiensEtMathematiques.01.Ang
33 reference(s) | 128-Le_Chat.01.Ang
33 reference(s) |
















![Tridimensional display of the Riemann Zeta function inside [-50.0,+50.0]x[-50.0,+50.0] Tridimensional display of the Riemann Zeta function inside [-50.0,+50.0]x[-50.0,+50.0]](../images/ZETA.21.M.D/timbre.jpg)
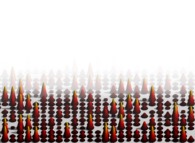
























![Tridimensional display of the Riemann Zeta function inside [-10.0,+20.0]x[-15.0,+15.0] (bird's-eye view) Tridimensional display of the Riemann Zeta function inside [-10.0,+20.0]x[-15.0,+15.0] (bird's-eye view)](../images/ZETA.11.m.D/timbre.jpg)








![Tridimensional display of the Riemann Zeta function inside [+0.1,+0.9]x[0,+50] Tridimensional display of the Riemann Zeta function inside [+0.1,+0.9]x[0,+50]](../images/ZETA.41.2.D/timbre.jpg)







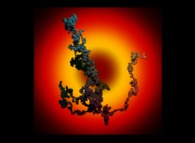




































![Tridimensional display of the Riemann Zeta function inside [-50.0,+50.0]x[-50.0,+50.0] (bird's-eye view) Tridimensional display of the Riemann Zeta function inside [-50.0,+50.0]x[-50.0,+50.0] (bird's-eye view)](../images/ZETA.21.m.D/timbre.jpg)