Les courbes remplissantes et au-delà :
Des carrés et des cubes aux surfaces (variétés bidimensionnelles) et aux variétés tridimensionnelles
CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[N'oubliez pas de visiter Une Machine Virtuelle à Explorer l'Espace-Temps et au-delà où vous trouverez plus de 10.000 images et animations à la frontière de l'Art et de la Science]
(Site WWW CMAP28 : cette page a été créée le 17/04/2023 et mise à jour le 03/10/2024 17:09:15 -CEST-)
[in english/en anglais]
Contenu :
1-Georg Cantor :
Dans la deuxième moitié du dix-neuvième siècle, Georg Cantor fut l'un des fondateurs
de la théorie des ensembles en s'interrogeant en particulier sur l'infini. Grâce à la
notion
d'ensemble des parties (c'est-à-dire l'ensemble de tous les sous-ensembles d'un ensemble donné),
il montra qu'il n'y avait pas un infini, mais une infinité.
Le plus petit infini est celui de l'ensemble des nombres entiers (N) : le dénombrable.
La notion de
bijection
entre deux ensembles est alors fondamentale : on dira que deux ensembles
ont le même cardinal ("ont la même taille") s'il existe une bijection entre eux. C'est ainsi que, presque paradoxalement,
les ensembles des nombres pairs, des rationnels, des
nombres algébriques,...
sont en bijection avec N et sont donc dénombrables.
Mais par une démonstration par l'absurde d'une étonnante simplicité, il montra qu'il n'en était pas de
même avec l'ensemble des nombres réels (R) :
R n'est pas dénombrable (le continu).
On notera que savoir s'il existe des ensembles de taille intermédiaire entre N et R est (malheureusement...) un
indécidable (appelé l'Hypothèse du Continu)
de la théorie ZFC (Zermelo, Fraenkel et axiome du Choix) des ensembles...
Au-delà de R il y a donc une infinité d'ensembles toujours plus énormes obtenus, par exemple, en
itérant la définition P d'ensemble des parties : {E,P(E),P(P(E)),...}.
Mais malgré cela, Georg Cantor a démontré
que R, R2,... Rn,... avaient même cardinal.
2-David Hilbert, Giuseppe Peano et les autres :
Partant de ce résultat, David Hilbert, Giuseppe Peano et d'autres encore ont imaginé
des courbes (paramétrées dans R) remplissant un carré (dans R2). Une façon simple de procéder consiste à partir d'une courbe dite
génératrice 
que l'on réduira et transformera en répétant cela une infinité de fois.
Pour illustrer ce processus, voici une
une courbe génératrice spécifique 
et les
quatre transformations 
qu'elle doit subir à chaque
itération.
Voici les cinq premières courbes bidimensionnelles de Hilbert avec un nombre croissant d'itérations
:
Voici quelques exemples de courbes bidimensionnelles de type Hilbert utilisant des courbes génératrices différentes
:
Ce procédé se généralise et il est ainsi possible de remplir un cube (dans R3)
à l'aide de courbes (toujours paramétrées dans R). Voici
l'une des courbes génératrices 
et de nouveau, une
courbe génératrice spécifique 
permet de comprendre les
huit transformations 
subies à chaque
itération.
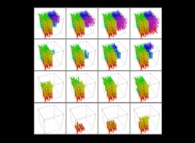
Voici les quatre premières courbes tridimensionnelles de Hilbert avec un nombre croissant d'itérations
:
Voici quelques exemples de courbes tridimensionnelles de type Hilbert utilisant des courbes génératrices différentes et
en particulier des nœuds "ouverts"
:
3-Surfaces tridimensionnelles (Variétés bidimensionnelles) :
De nombreuses surfaces -variétés bidimensionnelles- dans un espace tridimensionnel
peuvent être définies à l'aide d'un ensemble de trois équations :
X = Fx(u,v)
Y = Fy(u,v)
Z = Fz(u,v)
avec :
u ∈ [Umin,Umax]
v ∈ [Vmin,Vmax]
Par exemple :
Fx(u,v) = R.sin(u).cos(v)
Fy(u,v) = R.sin(u).sin(v)
Fz(u,v) = R.cos(u)
avec :
u ∈ [0,pi]
v ∈ [0,2.pi]
définit une sphère de rayon R centrée à l'origine.
[Umin,Umax]*[Vmin,Vmax] définit alors un domaine bidimensionnel rectangulaire D.
v ^
|
V |...... ---------------------------
max | |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
V |...... ---------------------------
min | : :
| : :
O------------------------------------------------->
U U u
min max
Définissons une courbe qui remplit le carré [0,1]x[0,1]
:
^
|
1 |---------------
| +++++ +++++ |
| + + + + |
| + +++++ + |
| + + |
| +++++ +++++ |
| + + |
| +++++ +++++ |
0 O------------------------>
0 1
Il est trivial de définir une correspondance entre le carré [0,1]x[0,1] et le domaine [Umin,Umax]*[Vmin,Vmax]
:
v ^
|
V |...... ---------------------------
max | | ++++++++ ++++++++ |
| | + + + + |
| | + + + + |
| | + +++++++++++ + |
| | + C + |
| | ++++++++ ++++++++ |
| | + + |
| | + + |
| | ++++++++ ++++++++ |
V |...... ---------------------------
min | : :
| : :
O------------------------------------------------->
U U u
min max
Il suffit alors de ne visualiser que les points {Fx(u,v),Fy(u,v),Fz(u,v)}
pour les couples {u,v} qui sont sur la courbe précédente C pour recouvrir la surface avec C....
Voici quelques exemples de ce processus
:
| Surface | ==> | Courbe C | ==> | Courbe recouvrant la surface |
 | ==> |  | ==> |  |
| | ==> |  | ==> |  |
| | ==> |  | ==> |  |
| | ==> |  | ==> |  |
| | ==> |  | ==> |  |
| | ==> |  | ==> |  |
| | ==> | | ==> |  |
| | ==> | | ==> |  |
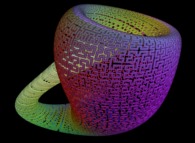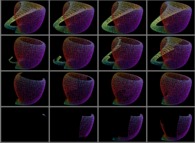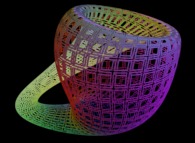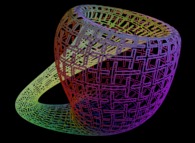4-Variétés tridimensionnelles :
De nombreuses variétés tridimensionnelles dans un espace tridimensionnel
peuvent être définies à l'aide d'un ensemble de trois équations :
X = Fx(u,v,w)
Y = Fy(u,v,w)
Z = Fz(u,v,w)
avec :
u ∈ [Umin,Umax]
v ∈ [Vmin,Vmax]
w ∈ [Wmin,Wmax]
[Umin,Umax]*[Vmin,Vmax]*[Wmin,Wmax] définit alors un domaine tridimensionnel rectangulaire D.
Il est trivial de généraliser le processus bidimensionnel précédent dans l'espace tridimensionnel...
Voici quelques exemples de ce processus
:
| Variété tridimensionnelle | ==> | Courbe C | ==> | Courbe remplissant la variété tridimensionnelle |
5-Au-delà :
Au lieu d'utiliser les courbes remplissantes pour remplir les domaines {u,v} et {u,v,w}, bi- et tridimensionnels,
on peut évidemment utiliser n'importe quelle autre méthode et, par exemple, les mouvements browniens
bi-
et tridimensionnel respectivement....
Voici quelques exemples de ces processus généralisés
:
Copyright © Jean-François COLONNA, 2023-2024.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2023-2024.
