Les courbes remplissantes de Hilbert et Peano et au-delà :
Des carrés et des cubes aux surfaces (variétés bidimensionnelles) et aux variétés tridimensionnelles
CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[N'oubliez pas de visiter Une Machine Virtuelle à Explorer l'Espace-Temps et au-delà où vous trouverez plus de 10.000 images et animations à la frontière de l'Art et de la Science]
(Site WWW CMAP28 : cette page a été créée le 03/01/2023 et mise à jour le 24/01/2025 18:15:23 -CET-)
[in english/en anglais]
Contenu :
1-La surjection bidimensionnelle de Peano :
Giuseppe Peano a défini la surjection suivante
:
[0,1] --> [0,1]x[0,1]
Soit T un nombre réel défini en base 3
:
T = 0.A1A2A3... ∈ [0,1] with Ai ∈ {0,1,2}
Soient X(T) et Y(T) deux fonctions réelles de T définie par
:
X(T) = 0.B1B2B3... ∈ [0,1] with Bi ∈ {0,1,2}
Y(T) = 0.C1C2C3... ∈ [0,1] with Ci ∈ {0,1,2}
avec
:
Bn = A2n-1 if A2+A4+...+A2n-0 is even
Bn = 2-A2n-1 otherwise
Cn = A2n if A1+A3+...+A2n-1 is even
Cn = 2-A2n otherwise
Ces deux fonctions X(T) et Y(T) définissent les coordonnées d'un point P(T) dans le carré [0,1]x[0,1].
La "courbe" visualisée -à l'aide de petites spères- est la trajectoire de P(T) lorsque T varie de 0 (en bas et à gauche) à 1-epsilon (en haut et à droite).
Voici les quatre premières courbes bidimensionnelles de Peano avec un nombre croissant de décimales
{2,4,6,8} :
[Voir les couleurs utilisées pour visualiser le paramètre T]
2-La surjection tridimensionnelle de Peano :
Une surjection tridimensionnelle peut être définie
:
[0,1] --> [0,1]x[0,1]x[0,1]
comme une généralisation de la version bidimensionnelle.
Soit T un nombre réel défini en base 3
:
T = 0.A1A2A3... ∈ [0,1] with Ai ∈ {0,1,2}
Soient X(T), Y(T) et Z(T) trois fonctions réelles de T définie par :
X(T) = 0.B1B2B3... ∈ [0,1] with Bi ∈ {0,1,2}
Y(T) = 0.C1C2C3... ∈ [0,1] with Ci ∈ {0,1,2}
Y(T) = 0.D1D2D3... ∈ [0,1] with Di ∈ {0,1,2}
avec
:
Bn = A3n-2 if A3+A6+...+A3n-0 is even
Bn = 2-A3n-2 otherwise
Cn = A3n-1 if A2+A5+...+A3n-1 is even
Cn = 2-A3n-1 otherwise
Dn = A3n if A1+A4+...+A3n-2 is even
Dn = 2-A3n otherwise
Ces trois fonctions X(T), Y(T) et Y(T) définissent les coordonnées d'un point P(T) dans le cube [0,1]x[0,1]x[0,1].
La "courbe" visualisée -à l'aide de petites spères- est la trajectoire de P(T) lorsque T varie de 0 (en bas et à gauche) à 1-epsilon (en haut et à droite).
Voici les trois premières courbes tridimensionnelles de Peano avec un nombre croissant de décimales
{3,6,9} :
[Voir les couleurs utilisées pour visualiser le paramètre T]
3-Les courbes de Hilbert bidimensionnelles :
Soit C1(T)
une courbe paramétrique
définie à l'aide de 2 fonctions réelles de T
(T ∈ [0,1])
X1(T) ∈ [0,1] et Y1(T) ∈ [0,1]
telles que
:
X1(T=0)=0 Y1(T=0)=0 (coin en bas et à gauche)
X1(T=1)=1 Y1(T=1)=0 (coin en bas et à droite)
On définit ensuite une suite de courbes Ci(T) (i >= 1) de la façon suivante
:
Ci(T) = {Xi(T),Yi(T)} ∈ [0,1]x[0,1] --> Ci+1(T) = {Xi+1(T),Yi+1(T)} ∈ [0,1]x[0,1]
if T ∈ [0,1/4[ :
Xi+1(T) = Yi(4T-0)
Yi+1(T) = Xi(4T-0)
Transformation 1
if T ∈ [1/4,2/4[ :
Xi+1(T) = Xi(4T-1)
Yi+1(T) = 1+Yi(4T-1)
Transformation 2
if T ∈ [2/4,3/4[ :
Xi+1(T) = 1+Xi(4T-2)
Yi+1(T) = 1+Yi(4T-2)
Transformation 3
if T ∈ [3/4,1] :
Xi+1(T) = 2-Yi(4T-3)
Yi+1(T) = 1-Xi(4T-3)
Transformation 4
Il convient de noter que 4=2d où d=2 est la dimension de l'espace.
Voir une courbe C1(T) 
spéciale afin de comprendre la signification géométrique des 4 transformations 
et de leur ordre 
.
Voici les cinq premières courbes bidimensionnelles de Hilbert avec un nombre croissant d'itérations
:
[Voir les couleurs utilisées pour visualiser le paramètre T]
Voir la construction de quelques unes d'entre-d'elles
:
Voici quelques exemples de courbes bidimensionnelles de type Hilbert utilisant des courbes génératrices différentes
:
Voici le "mapping" de quelques images à l'aide d'une courbe bidimensionnelle de Hilbert :
:
 | ==>
[itération 11] |  |
 | ==>
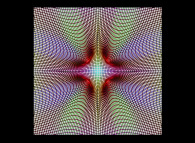[itération 10] |  |
 | ==>
[itération 9] |  |
 | ==>
[itération 10] |  |
4-Les courbes de Hilbert tridimensionnelles :
Soit C1(T)
une courbe paramétrique
définie à l'aide de 3 fonctions réelles de T
(T ∈ [0,1])
X1(T) ∈ [0,1], Y1(T) ∈ [0,1] et Z1(T) ∈ [0,1]
telles que
:
X1(T=0)=0 Y1(T=0)=0 Z1(T=0)=0 (coin en bas et à gauche au premier plan)
X1(T=1)=1 Y1(T=1)=0 Z1(T=1)=0 (coin en bas et à droite au premier plan)
On définit ensuite une suite de courbes Ci(T) (i >= 1) de la façon suivante
:
Ci(T) = {Xi(T),Yi(T),Zi(T)} ∈ [0,1]x[0,1]x[0,1] --> Ci+1(T) = {Xi+1(T),Yi+1(T),Zi+1(T)} ∈ [0,1]x[0,1]x[0,1]
if T ∈ [0,1/8[ :
Xi+1(T) = Xi(8T-0)
Yi+1(T) = Zi(8T-0)
Zi+1(T) = Yi(8T-0)
Transformation 1
if T ∈ [1/8,2/8[ :
Xi+1(T) = Zi(8T-1)
Yi+1(T) = 1+Yi(8T-1)
Zi+1(T) = Xi(8T-1)
Transformation 2
if T ∈ [2/8,3/8[ :
Xi+1(T) = 1+Xi(8T-2)
Yi+1(T) = 1+Yi(8T-2)
Zi+1(T) = Zi(8T-2)
Transformation 3
if T ∈ [3/8,4/8[ :
Xi+1(T) = 1+Zi(8T-3)
Yi+1(T) = 1-Xi(8T-3)
Zi+1(T) = 1-Yi(8T-3)
Transformation 4
if T ∈ [4/8,5/8[ :
Xi+1(T) = 2-Zi(8T-4)
Yi+1(T) = 1-Xi(8T-4)
Zi+1(T) = 1+Yi(8T-4)
Transformation 5
if T ∈ [5/8,6/8[ :
Xi+1(T) = 1+Xi(8T-5)
Yi+1(T) = 1+Yi(8T-5)
Zi+1(T) = 1+Zi(8T-5)
Transformation 6
if T ∈ [6/8,7/8[ :
Xi+1(T) = 1-Zi(8T-6)
Yi+1(T) = 1+Yi(8T-6)
Zi+1(T) = 2-Xi(8T-6)
Transformation 7
if T ∈ [7/8,1] :
Xi+1(T) = Xi(8T-7)
Yi+1(T) = 1-Zi(8T-7)
Zi+1(T) = 2-Yi(8T-7)
Transformation 8
Il convient de noter que 8=2d où d=3 est la dimension de l'espace.
Voir une courbe C1(T) 
spéciale afin de comprendre la signification géométrique des 8 transformations 
et de leur ordre 
.
Voici les quatre premières courbes tridimensionnelles de Hilbert avec un nombre croissant d'itérations
:
[Voir les couleurs utilisées pour visualiser le paramètre T]
Voir la construction de l'une d'elles
:
Voici quelques exemples de courbes tridimensionnelles de type Hilbert utilisant des courbes génératrices différentes et
en particulier des nœuds "ouverts"
:
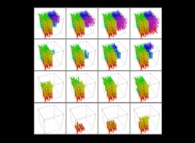
[More information about Peano Curves and Infinite Knots -in english/en anglais-]
[Plus d'informations à propos des Courbes de Peano et des Nœuds Infinis -en français/in french-]
5-Surfaces tridimensionnelles (Variétés bidimensionnelles) :
De nombreuses surfaces -variétés bidimensionnelles- dans un espace tridimensionnel
peuvent être définies à l'aide d'un ensemble de trois équations :
X = Fx(u,v)
Y = Fy(u,v)
Z = Fz(u,v)
avec :
u ∈ [Umin,Umax]
v ∈ [Vmin,Vmax]
Par exemple :
Fx(u,v) = R.sin(u).cos(v)
Fy(u,v) = R.sin(u).sin(v)
Fz(u,v) = R.cos(u)
avec :
u ∈ [0,pi]
v ∈ [0,2.pi]
définit une sphère de rayon R centrée à l'origine.
[Umin,Umax]*[Vmin,Vmax] définit alors un domaine bidimensionnel rectangulaire D.
v ^
|
V |...... ---------------------------
max | |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
| |+++++++++++++++++++++++++++|
V |...... ---------------------------
min | : :
| : :
O------------------------------------------------->
U U u
min max
Définissons une courbe qui remplit le carré [0,1]x[0,1]
:
^
|
1 |---------------
| +++++ +++++ |
| + + + + |
| + +++++ + |
| + + |
| +++++ +++++ |
| + + |
| +++++ +++++ |
0 O------------------------>
0 1
Il est trivial de définir une correspondance entre le carré [0,1]x[0,1] et le domaine [Umin,Umax]*[Vmin,Vmax]
:
v ^
|
V |...... ---------------------------
max | | ++++++++ ++++++++ |
| | + + + + |
| | + + + + |
| | + +++++++++++ + |
| | + C + |
| | ++++++++ ++++++++ |
| | + + |
| | + + |
| | ++++++++ ++++++++ |
V |...... ---------------------------
min | : :
| : :
O------------------------------------------------->
U U u
min max
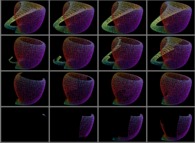
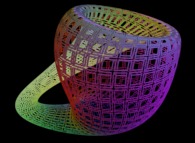
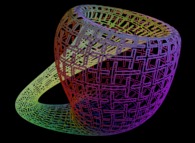
Il suffit alors de ne visualiser que les points {Fx(u,v),Fy(u,v),Fz(u,v)}
pour les couples {u,v} qui sont sur la courbe précédente C pour recouvrir la surface avec C....
Voici quelques exemples de ce processus
:
| Surface | ==> | Courbe C | ==> | Courbe recouvrant la surface |
 | ==> |  | ==> |  |
| | ==> | | ==> |  |
| | ==> | | ==> |  |
| | ==> |  | ==> |  |
| | ==> |  | ==> |  |
| | ==> |  | ==> |  |
| | ==> |  | ==> |  |
| | ==> | | ==> |  |
| | ==> | | ==> |  |
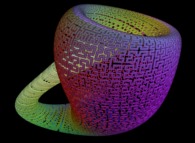6-Variétés tridimensionnelles :
De nombreuses variétés tridimensionnelles dans un espace tridimensionnel
peuvent être définies à l'aide d'un ensemble de trois équations :
X = Fx(u,v,w)
Y = Fy(u,v,w)
Z = Fz(u,v,w)
avec :
u ∈ [Umin,Umax]
v ∈ [Vmin,Vmax]
w ∈ [Wmin,Wmax]
[Umin,Umax]*[Vmin,Vmax]*[Wmin,Wmax] définit alors un domaine tridimensionnel rectangulaire D.
Il est trivial de généraliser le processus bidimensionnel précédent dans l'espace tridimensionnel...
Voici quelques exemples de ce processus
:
| Variété tridimensionnelle | ==> | Courbe C | ==> | Courbe remplissant la variété tridimensionnelle |
7-Au-delà :
Au lieu d'utiliser les courbes remplissantes pour remplir les domaines {u,v} et {u,v,w}, bi- et tridimensionnels,
on peut évidemment utiliser n'importe quelle autre méthode et, par exemple, les mouvements browniens
bi-
et tridimensionnel respectivement....
Voici quelques exemples de ces processus généralisés
:
Copyright © Jean-François COLONNA, 2023-2025.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2023-2025.
