Comprendre L'Expérimentation Virtuelle jusqu'à ses Limites
CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
france telecom, France Telecom R&D
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[N'oubliez pas de visiter Une Machine Virtuelle à Explorer l'Espace-Temps et au-delà où vous trouverez plus de 10.000 images et animations à la frontière de l'Art et de la Science]
(Site WWW CMAP28 : cette page a été créée le 28/10/2002 et mise à jour le 19/03/2025 13:32:34 -CET-)
(Texte de la conférence inaugurale du Congrès National des Professeurs de Mathématiques de l'Enseignement Public, Rennes, 26/10/2002)
Résumé : Après avoir rappelé en quoi consiste l'Expérimentation dite Réelle,
ce texte définit l'Expérimentation Virtuelle,
nouvelle approche de la connaissance scientifique. Ses
avantages sont décrits et illustrés à
l'aide de quelques exemples empruntés, en particulier, à la
Mécanique Quantique, à la Géométrie Fractale et à la Mécanique Céleste. Ses
dangers liés, principalement à la programmation, aux erreurs
d'arrondi et aux modes de représentation,
sont exposés en détail.
Mots-Clefs :
Anaglyphes,
Art et Science,
Autostéréogrammes,
Chaos Déterministe,
Création Artistique,
Entrelacs,
Erreurs d'arrondi,
Expérimentation Virtuelle,
Génie Logiciel,
Géométrie Fractale,
Infographie,
Mathématiques,
Mécanique Céleste,
Mécanique Quantique,
Physique,
Sensibilité aux Erreurs d'Arrondi,
Simulation Numérique,
Stéréogrammes,
Synthèse de Phénomènes Naturels,
Synthèse de Texture,
Visualisation Scientifique,
Voyage Virtuel dans l'Espace-Temps.
Plan de ce document :
1-L'EXPERIMENTATION REELLE :
Lever et coucher du Soleil ou encore
chute inexorable des pommes : depuis la
nuit des temps l'homme observe les relations,
les régularités et les symétries de son univers.
Le sens de la vision, certainement à l'origine de la curiosité scientifique,
joue ici un rôle essentiel grâce d'une part à sa "portée infinie" (que serait d'ailleurs notre science
si nous n'étions doté que de l'ouïe et du toucher ?) et, d'autre part, à ses performances exceptionnelles
dans le domaine de la reconnaissance des formes dans un environnement quelconque, changeant et bruité.
Pour décrire, structurer et transmettre ces relations, ces régularités et ces symétries,
en particulier dans le domaine de la physique,
c'est le langage des mathématiques qui est utilisé et aujourd'hui,
toutes les grandes lois de la nature sont
exprimées sous la forme d'équations qui
n'ont bien souvent pas d'équivalents dans
nos langues naturelles.
Bien que d'une efficacité tout à la fois redoutable et énigmatique, nos Mathématiques ne sont peut-être que le reflet de nos structures cognitives et non point l'ultime réalité platonicienne.
Mais les équations ainsi obtenues ne font pas qu'engranger des
connaissances ; elles permettent aussi d'en
produire de nouvelles.
Donnons quelques exemples historiques :
- En 1846, Urbain Le Verrier découvre, à partir
des équations de la mécanique newtonienne, la planète Neptune. Les instruments de mesure
progressant, eux-aussi, de petites différences étaient apparues
entre les observations astronomiques et les calculs. Plutôt que de vouloir remplacer une
mécanique qui donnait malgré tout d'aussi bons résultats, Urbain Le Verrier
imagina que notre connaissance du système solaire était alors incomplète et calcula
les caractéristiques d'une certaine planète manquante qui fut ensuite effectivement observée.
Malheureusement une telle démarche ne suffit pas à expliquer ultérieurement les anomalies concernant
Mercure et seule une révolution en eu raison...
- En 1915, Albert Einstein, utilisant sa théorie
de la Relativité Générale, prévoit la déviation des
rayons lumineux par la matière et c'est en 1919, au
cours d'une éclipse restée fameuse, que Sir Arthur
Stanley Eddington vérifiait, par la mesure, les
prévisions d'Albert Einstein, ce qui lui valu alors une célébrité planètaire.
Grâce à sa théorie, par la suite,
furent imaginés les trous noirs ou encore une origine possible de notre espace et
de notre temps : le Big Bang que des expériences actuelles semblent
confirmer.
- En 1930, Paul Dirac annonce l'existence de
l'anti-électron grâce à la Mécanique Quantique. Plus tard, faisant suite
au fameux paradoxe EPR (Einstein, Podolsky et Rosen) il y eu le théorème de Bell
et les expériences d'Alain Aspect à l'Institut d'Optique d'Orsay et l'humanité découvrait le
caractère non séparable de la Réalité...
Ces quelques exemples illustrent bien le "miracle" des Mathématiques qui ont ainsi le pouvoir
de nous entrainer bien au-delà de nos sens et de notre intuition...
Mais bien évidemment, ses prédictions n'ont de sens
que si elles sont ensuite confrontées à
l'expérience ; une théorie scientifique se
devant d'être, par essence, réfutable.
Ainsi le chercheur observe, modélise et expérimente.
Des modèles mathématiques vont
donc décrire le comportement des systèmes
que les chercheurs et les ingénieurs étudient (par la suite, nous n'examinerons pas le cas
de la recherche industrielle ; mais en fait tout ce qui sera dit concernant la recherche fondamentale
pourra être transposé, sans difficulté, aux domaines plus appliqués) ; il s'agit donc
en quelque sorte d'une analogie : un système et son modèle, à un niveau d'observation donné
et dans les mêmes conditions expérimentales,
doivent produire, pour les grandeurs physiques caractéristiques, des valeurs égales (à epsilon près...).
Pour un système donné, le modèle qui est sensé le
décrire contient des équations reliant
entre-elles ces différentes grandeurs
(par exemple des coordonnées), des conditions
initiales (donnant certaines valeurs à l'instant 0) et
enfin des conditions aux limites (précisant, par
exemple, ce qui se passe aux frontières du domaine à
l'intérieur duquel se fait l'étude).
Ainsi qu'il est facile de l'imaginer, ils sont
en général d'une très grande complexité ;
leur étude pourra donc présenter des
difficultés tant théoriques que techniques,
parfois insurmontables, dont l'annexe 1
donne un apercu. Que faire ? Sommes-nous
alors dans une impasse ?
2-DEFINITION DE L'EXPERIMENTATION VIRTUELLE :
Sans remonter jusqu'aux automates de Vaucanson ou encore au métier à tisser
de Jacquard, c'est au
milieu du dix-neuvième siècle que Charles Babbage, aidé de sa
collaboratrice Lady Ada Lovelace (fille de Lord Byron et premier programmeur de l'histoire de l'humanité),
imagina une machine numérique programmable. Malheureusement n'ayant à sa disposition
que des systèmes mécaniques, il faudra attendre la seconde
guerre mondiale et les travaux de John Von Neumann, Alan Turing
et beaucoup d'autres, pour voir se
développer les premiers ordinateurs électroniques, grâce
auxquels, aujourd'hui, nous sommes
capables de calculer tout et parfois n'importe
quoi, comme nous le verrons par la suite.
Dès l'origine, John Von Neumann avait imaginé la possibilité
de faire des expériences numériques grâce aux ordinateurs. Mais
les machines des années quarante n'avaient ni les performances,
ni l'ergonomie des machines d'aujourd'hui.
A titre d'exemple, cet ordinateur  , qui fut le premier
dont l'auteur a pu disposer à titre professionnel en 1972, disposait, à l'intérieur de
ses armoires de trois mètres cubes, d'une "phénoménale" mémoire centrale de 32 kilo-octets
et de trois disques durs de chacun un demi méga-octet !
Aujourd'hui (au mois de novembre 2002), les ordinateurs portables les plus performants
disposent d'horloges de deux giga-hertz,
intégrent des mémoires centrales d'un giga-octet (Go) et des disques de plusieurs dizaines de Go.
Il semble que cette course aux performances soit faite pour se poursuivre dans les années à venir.
Evidemment, la technonologie actuelle possède des limites, mais celles-ci
sont relativement éloignées (et d'ailleurs l'histoire montre qu'elles sont fréquemment repoussées...).
D'autre part, de nouvelles façons d'utiliser les ordinateurs permettent d'atteindre
des capacités de traitement et de stockage absolument phénoménales. C'est en particulier
le cas avec la notion de méta-ordinateur
qui permet de concevoir des systèmes virtuels répartis (éventuellement sur la Terre entière)
n'utilisant que des systèmes standards et bon marché.
Et au-delà, les recherches les plus avancées nous annoncent
l'ordinateur quantique, mais
pourra-t-il être construit au-delà de quelques prototypes de laboratoire capables actuellement
de factoriser de petits nombres à deux chiffres (il convient de rappeler que l'un des attraits
de ces machines, reposant sur le principe de superposition linéaire cher à la Mécanique Quantique,
est d'offrir, par rapport aux machines "classiques", la possibilité de factoriser
beaucoup plus rapidement les nombres entiers -algorithme de Schorr-, avec des conséquences
évidentes en ce qui concerne de nombreuses méthodes de chiffrement...) ?
, qui fut le premier
dont l'auteur a pu disposer à titre professionnel en 1972, disposait, à l'intérieur de
ses armoires de trois mètres cubes, d'une "phénoménale" mémoire centrale de 32 kilo-octets
et de trois disques durs de chacun un demi méga-octet !
Aujourd'hui (au mois de novembre 2002), les ordinateurs portables les plus performants
disposent d'horloges de deux giga-hertz,
intégrent des mémoires centrales d'un giga-octet (Go) et des disques de plusieurs dizaines de Go.
Il semble que cette course aux performances soit faite pour se poursuivre dans les années à venir.
Evidemment, la technonologie actuelle possède des limites, mais celles-ci
sont relativement éloignées (et d'ailleurs l'histoire montre qu'elles sont fréquemment repoussées...).
D'autre part, de nouvelles façons d'utiliser les ordinateurs permettent d'atteindre
des capacités de traitement et de stockage absolument phénoménales. C'est en particulier
le cas avec la notion de méta-ordinateur
qui permet de concevoir des systèmes virtuels répartis (éventuellement sur la Terre entière)
n'utilisant que des systèmes standards et bon marché.
Et au-delà, les recherches les plus avancées nous annoncent
l'ordinateur quantique, mais
pourra-t-il être construit au-delà de quelques prototypes de laboratoire capables actuellement
de factoriser de petits nombres à deux chiffres (il convient de rappeler que l'un des attraits
de ces machines, reposant sur le principe de superposition linéaire cher à la Mécanique Quantique,
est d'offrir, par rapport aux machines "classiques", la possibilité de factoriser
beaucoup plus rapidement les nombres entiers -algorithme de Schorr-, avec des conséquences
évidentes en ce qui concerne de nombreuses méthodes de chiffrement...) ?
Une Expérience Virtuelle sera une expérience effectuée non pas sur
un système "réel", mais bien plutôt sur son modèle mathématique traduit en un ou plusieurs
programmes executés dans la mémoire d'ordinateurs (le mot virtuel ayant été
choisi en tant que l'un des antonymes de réel).
Des méthodes dites numériques seront en général nécessaires
afin de connaitre la solution des
équations, non point sous la forme générale
de formules inexistantes ou inaccessibles,
mais sous celle particulière de valeurs
numériques. Cette situation ne doit
d'ailleurs pas nous choquer. N'oublions pas
que l'acte fondamental du scientifique est la
mesure : la réalité ne se manifeste à lui, au
cours des expériences, que par
l'intermédiaire de nombres (des
coordonnées, des vitesses, des
températures,...) ; il n'a jamais accès aux
formules du "Vieux" (pour paraphraser
Albert Einstein...).
Que faire alors des résultats obtenus ?
Dans la cas du problème des N-corps
(revoir l'annexe 1), la situation n'est pas
dramatique, puisque le nombre de valeurs
obtenues n'excède pas quelques dizaines de
milliers. Malgré cela, la contemplation de
celles-ci ne révélerait pas aisément ce qui, en
fait, saute immédiatement aux yeux
lorsqu'elles sont mises en images d'une
façon tout à fait naturelle (c'est-à-dire telle
que les corps étudiés seraient perçus dans
l'espace physique). Par exemple, cette figure  montre instantanément et sans effort de
réflexion, que les trajectoires de ce problème à quatre corps utilisant
les conditions initiales suivantes (données en unités MKSA et visualisées en bas et à gauche de cette matrice de 16 images) :
montre instantanément et sans effort de
réflexion, que les trajectoires de ce problème à quatre corps utilisant
les conditions initiales suivantes (données en unités MKSA et visualisées en bas et à gauche de cette matrice de 16 images) :
C1={0,0,0}, V1={0,0,0}, M1=1030,
C2={26.1010,0,0}, V2={0,-133.102,0}, M2=1028,
C3={-8.1011,0,0}, V3={0,5.103,0}, M3=2.1027,
C4={-8.1011,5.1010,0}, V4={-960,5.103,0}, M4=735.1020
(où Ck, Vk et Mk représentent respectivement les
coordonnées, la vitesse et la masse du corps numéro k)
ne sont pas
des ellipses, et même, ne sont pas
périodiques. Il est alors évident, que dans
des situations fréquentes, ou le volume des
résultats s'exprime en milliards de nombres (ou
davantage encore), le recours à l'image de
synthèse est incontournable. De plus, ainsi
que cela fut rappelé précedemment, l'acte de
mesure est fondamental ; les expériences qui
sont actuellement menées, par exemple,
avec les accélérateurs de particules ou les
télescopes, donnent elles aussi des
"montagnes" de résultats numériques.
L'image de synthèse est donc tout aussi utile
dans ce contexte. Il n'est certainement pas
exagéré de dire qu'elle est aux expériences
d'aujourd'hui ce que l'aiguille des
appareils de mesures était aux expériences
d'hier.
3-QUELQUES EXEMPLES D'EXPERIENCES VIRTUELLES :
3.1-La Mécanique Quantique :
L'expérimentation virtuelle va nous permettre de manipuler et de voir des objets
autrement inaccessibles.
Voici quelques exemples allant de la théorie des supercordes à l'atome d'hydrogène :
-
 Représentation tridimensionnelle d'une variété quadridimensionnelle de Calabi-Yau
: la théorie des supercordes est actuellement la solution la plus
prometteuse en ce qui concerne l'unification de la Mécanique Quantique
(les interactions fortes et électrofaibles) et de la
Relativité Générale (interaction gravitationnelle).
Elle demande pour cela sept dimensions supplémentaires "à côté" des
quatre dimensions (trois d'espace et une de temps) que nous percevons.
Ces sept dimensions, auxquelles nous ne sommes pas sensibles,
seraient organisées selon des variétés de Calabi-Yau,
dont la "forme" et la topologie conditionneraient notre Physique
(nombre de familles de particules élémentaires -3- et leurs propriétés,
en particulier).
Représentation tridimensionnelle d'une variété quadridimensionnelle de Calabi-Yau
: la théorie des supercordes est actuellement la solution la plus
prometteuse en ce qui concerne l'unification de la Mécanique Quantique
(les interactions fortes et électrofaibles) et de la
Relativité Générale (interaction gravitationnelle).
Elle demande pour cela sept dimensions supplémentaires "à côté" des
quatre dimensions (trois d'espace et une de temps) que nous percevons.
Ces sept dimensions, auxquelles nous ne sommes pas sensibles,
seraient organisées selon des variétés de Calabi-Yau,
dont la "forme" et la topologie conditionneraient notre Physique
(nombre de familles de particules élémentaires -3- et leurs propriétés,
en particulier).
-
 Structure en quarks et gluons du nucléon
: le nucléon (proton ou neutron) n'est pas une particule élémentaire.
Il est constitué de trois quarks dits de valence
(de saveur UUD et UDD pour le proton
et le neutron respectivement)
et d'une mer de particules virtuelles (quarks et gluons) en interaction.
Interrogeons nous, dès à présent, sur la signification des formes
et des couleurs utilisées dans cette image : quel sens ont-elles à cette
échelle (1.0E-15 mètre) ?
Structure en quarks et gluons du nucléon
: le nucléon (proton ou neutron) n'est pas une particule élémentaire.
Il est constitué de trois quarks dits de valence
(de saveur UUD et UDD pour le proton
et le neutron respectivement)
et d'une mer de particules virtuelles (quarks et gluons) en interaction.
Interrogeons nous, dès à présent, sur la signification des formes
et des couleurs utilisées dans cette image : quel sens ont-elles à cette
échelle (1.0E-15 mètre) ?
-
 Visualisation tridimensionnelle de la superposition linéaire de 6 états propres de l'atome d'Hydrogène (calcul tridimensionnel). L'hydrogène, le plus simple des atomes, bien
qu'il soit parfaitement connu dans le cadre de la Mécanique
Quantique, peut encore nous révéler bien des choses. Cette
image est extraite d'une séquence représentant l'évolution au cours du
temps, dans certaines conditions qu'il n'est pas utile de
préciser ici, de la densité de probabilité de présence de l'électron dans
l'espace physique. Celle-ci est codée à l'aide de la luminance
de chacun des points de l'image : plus un point est lumineux,
plus l'électron à de chance de se trouver sur la ligne de visée
joignant l'œil de l'observateur à ce point. Cette animation a une
vocation pédagogique et fut realisée en collaboration avec
Jean-Louis Basdevant pour le cours de Mécanique Quantique
qu'il enseigne à l'Ecole Polytechnique.
Visualisation tridimensionnelle de la superposition linéaire de 6 états propres de l'atome d'Hydrogène (calcul tridimensionnel). L'hydrogène, le plus simple des atomes, bien
qu'il soit parfaitement connu dans le cadre de la Mécanique
Quantique, peut encore nous révéler bien des choses. Cette
image est extraite d'une séquence représentant l'évolution au cours du
temps, dans certaines conditions qu'il n'est pas utile de
préciser ici, de la densité de probabilité de présence de l'électron dans
l'espace physique. Celle-ci est codée à l'aide de la luminance
de chacun des points de l'image : plus un point est lumineux,
plus l'électron à de chance de se trouver sur la ligne de visée
joignant l'œil de l'observateur à ce point. Cette animation a une
vocation pédagogique et fut realisée en collaboration avec
Jean-Louis Basdevant pour le cours de Mécanique Quantique
qu'il enseigne à l'Ecole Polytechnique.
Ces quelques images ne peuvent pas ne pas nous intriguer ; en effet,
les "objets" ici représentés relèvent de la Mécanique Quantique, laquelle nous
interdit, par exemple, de connaître simultanément avec une infinie
précision la position et la vitesse d'une particule, ce qu'elles semblent montrer malgré tout.
De plus, quelles significations ont les formes et les couleurs utilisées, alors que ces
notions n'ont aucun sens à cette échelle ? Nous reviendrons ultérieurement sur ces problèmes...
3.2-La Géométrie Fractale :
L'Expérimentation Virtuelle va aussi nous permettre de reproduire des fragments de Réalité "intuitive".
Les premières courbes continues non différentiables apparurent à la fin du dix-neuvième siècle,
nées de l'imagination de Weierstrass -peut-être le pionnier-, Cantor, Peano,
Lebesgue, Hausdorff, Besicovitch, von Koch, Sierpinski,...
Mais il fallu attendre la fin des années soixante pour que Benoît Mandelbrot réveillent ces "monstres"
assoupis et en montre l'utilité [Plus d'informations...].
3.2.1-La Géométrie Fractale Déterministe :
Pour ces objets, le hasard n'intervient pas.
-
 Les deux premières itérations de la construction de la courbe de von Koch. Il s'agit là du plus simple des objets fractals.
Malgré cela, il en possède toutes les propriétés : d'une
part l'autosimilarité (l'objet est invariant par
homothétie) et d'autre part le fini et l'infini s'y cotoie (bien que
cette courbe réside dans un domaine fini, à chaque itération sa longueur
est multipliée par 4/3 et tend donc vers l'infini ; par exemple, partant
d'un segment -bleu- d'un mètre de long, au bout de 90 itérations
la longueur est supérieure à la distance de la Terre au Soleil !).
Les deux premières itérations de la construction de la courbe de von Koch. Il s'agit là du plus simple des objets fractals.
Malgré cela, il en possède toutes les propriétés : d'une
part l'autosimilarité (l'objet est invariant par
homothétie) et d'autre part le fini et l'infini s'y cotoie (bien que
cette courbe réside dans un domaine fini, à chaque itération sa longueur
est multipliée par 4/3 et tend donc vers l'infini ; par exemple, partant
d'un segment -bleu- d'un mètre de long, au bout de 90 itérations
la longueur est supérieure à la distance de la Terre au Soleil !).
-
 Le long de la frontière de l'ensemble de Mandelbrot. L'ensemble de Mandelbrot
et les ensembles de Julia
sont ici définis dans le plan Complexe.
Le long de la frontière de l'ensemble de Mandelbrot. L'ensemble de Mandelbrot
et les ensembles de Julia
sont ici définis dans le plan Complexe.
-
 L'ensemble de Julia dans le corps des quaternions calculé pour A=(0,1,0,0) -ou 'la danseuse d'Yr'- -section tridimensionnelle-. Les itérations dans le plan Complexe peuvent
être étendues sans difficultés au corps des Quaternions.
La difficulté est alors plus au niveau de la représentation,
puisqu'il s'agit alors d'objets quadrimensionnels.
L'ensemble de Julia dans le corps des quaternions calculé pour A=(0,1,0,0) -ou 'la danseuse d'Yr'- -section tridimensionnelle-. Les itérations dans le plan Complexe peuvent
être étendues sans difficultés au corps des Quaternions.
La difficulté est alors plus au niveau de la représentation,
puisqu'il s'agit alors d'objets quadrimensionnels.
-
 Ensembles de Julia dans le corps des quaternions lors d'une promenade autour de l'ensemble de Mandelbrot -coupes tridimensionnelles-.
Ensembles de Julia dans le corps des quaternions lors d'une promenade autour de l'ensemble de Mandelbrot -coupes tridimensionnelles-.
-
 Rotation de 2.pi autour des axes Y et Z d'un ensemble de Julia dans le corps des quaternions -section tridimensionnelle-. La visualisation d'un ensemble de Julia calculé
dans le corps des Quaternions présente donc des difficultés
considérables. Il n'est évidemment pas question ici de représenter
directement ses quatre dimensions, puisque nous évoluons
dans un espace aux apparences tridimensionnelles. Un ou plusieurs artifices
doivent donc être utilisés : dans ce cas précis, seules sont
visualisées seize sections tridimensionnelles obtenues au
cours d'une rotation de 2 pi autour de l'un de ses axes. Cette
opération, difficile à imaginer, peut être mieux comprise
en l'appliquant à un objet de notre espace physique : prenons,
par exemple, un cylindre que nous représenterions par une
coupe effectuée à l'aide d'un plan arbitraire. Si nous
observons l'image de celle-ci alors que le cylindre est en
rotation, nous verrons une figure géométrique bidimensionnelle
se déformer et présenter alternativement l'apparence d'un rectangle et d'une
ellipse, suivant l'orientation du plan de coupe par rapport à l'axe du cylindre.
C'est ce qui est montré ici, le cylindre étant remplacé
par un objet fractal à quatre dimensions, et le plan par un
hyperplan tridimensionnel...
Rotation de 2.pi autour des axes Y et Z d'un ensemble de Julia dans le corps des quaternions -section tridimensionnelle-. La visualisation d'un ensemble de Julia calculé
dans le corps des Quaternions présente donc des difficultés
considérables. Il n'est évidemment pas question ici de représenter
directement ses quatre dimensions, puisque nous évoluons
dans un espace aux apparences tridimensionnelles. Un ou plusieurs artifices
doivent donc être utilisés : dans ce cas précis, seules sont
visualisées seize sections tridimensionnelles obtenues au
cours d'une rotation de 2 pi autour de l'un de ses axes. Cette
opération, difficile à imaginer, peut être mieux comprise
en l'appliquant à un objet de notre espace physique : prenons,
par exemple, un cylindre que nous représenterions par une
coupe effectuée à l'aide d'un plan arbitraire. Si nous
observons l'image de celle-ci alors que le cylindre est en
rotation, nous verrons une figure géométrique bidimensionnelle
se déformer et présenter alternativement l'apparence d'un rectangle et d'une
ellipse, suivant l'orientation du plan de coupe par rapport à l'axe du cylindre.
C'est ce qui est montré ici, le cylindre étant remplacé
par un objet fractal à quatre dimensions, et le plan par un
hyperplan tridimensionnel...
3.2.2-La Géométrie Fractale Non Déterministe :
De nombreux objets de la nature possèdent (approximativement)
la propriéte d'autosimilarité ; c'est le cas des côtes maritimes,
des montagnes, des nuages, de certaines plantes,...
Ils peuvent donc être modélisés à l'aide de la géométrie fractale,
à condition d'y introduire de l'aléatoire.
-
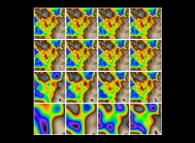 Le processus itératif de génération de champs fractals bidimensionnels (16 itérations). Il consiste à rajouter, à chaque nouvelle itération,
des détails, identiques statistiquement à ceux
ajoutés aux itérations précédentes, mais à une échelle inférieure
[Plus d'informations...].
Le processus itératif de génération de champs fractals bidimensionnels (16 itérations). Il consiste à rajouter, à chaque nouvelle itération,
des détails, identiques statistiquement à ceux
ajoutés aux itérations précédentes, mais à une échelle inférieure
[Plus d'informations...].
-
 Le processus itératif de génération de montagnes fractales (16 itérations).
Le processus itératif de génération de montagnes fractales (16 itérations).
-
 Montagnes au lever du Soleil.
Montagnes au lever du Soleil.
-
 Montagnes et dynamique de nuages légers -cette séquence étant périodique-. Toutes ces images sont en fait des coupes
tridimensionnelles dans des objets fractals
quadrimensionnels ; cela permet d'envisager divers
types d'animations.
Montagnes et dynamique de nuages légers -cette séquence étant périodique-. Toutes ces images sont en fait des coupes
tridimensionnelles dans des objets fractals
quadrimensionnels ; cela permet d'envisager divers
types d'animations.
-
 L'érosion de la Tour de Babel.
L'érosion de la Tour de Babel.
-
 Tremblement de terre sur des montagnes multi-fractales.
Tremblement de terre sur des montagnes multi-fractales.
-
 Monument Valley au lever du Soleil. Des contraintes diverses peuvent être appliquées ;
cela permet ainsi de reproduire des reliefs connus
(dans le cas présent, il n'y a quasiment que
des basses et des hautes altitudes).
Monument Valley au lever du Soleil. Des contraintes diverses peuvent être appliquées ;
cela permet ainsi de reproduire des reliefs connus
(dans le cas présent, il n'y a quasiment que
des basses et des hautes altitudes).
-
 Monument Valley dansante.
Monument Valley dansante.
-
 L'anomalie de Botticelli sur la Lune. En exploitant plusieurs fois le modèle simultanément,
il est possible de reconstituer les trois types de relief présents
à la surface de la Lune (les montagnes, les failles
dans les mers et les cratères). Afin de "signer" la nature
synthétique de cette image, un relief anthropomorphique
(le visage de Flore dans le Printemps de Botticelli)
a été ajouté au centre et à droite du relief.
L'anomalie de Botticelli sur la Lune. En exploitant plusieurs fois le modèle simultanément,
il est possible de reconstituer les trois types de relief présents
à la surface de la Lune (les montagnes, les failles
dans les mers et les cratères). Afin de "signer" la nature
synthétique de cette image, un relief anthropomorphique
(le visage de Flore dans le Printemps de Botticelli)
a été ajouté au centre et à droite du relief.
-
 Structure fractale tridimensionnelle. Il est intéressant de noter au sujet de cette image
qu'elle est issue des mêmes valeurs numériques que la plupart
des images précédentes, l'apparence visuelle très
différente venant d'un autre choix de mode de représentation.
Il s'agit là d'un problème très général, sur lequel nous
reviendrons plus tard : en toute généralité, il y a de
très nombreuses façons de représenter un même ensemble
de valeurs numériques.
Structure fractale tridimensionnelle. Il est intéressant de noter au sujet de cette image
qu'elle est issue des mêmes valeurs numériques que la plupart
des images précédentes, l'apparence visuelle très
différente venant d'un autre choix de mode de représentation.
Il s'agit là d'un problème très général, sur lequel nous
reviendrons plus tard : en toute généralité, il y a de
très nombreuses façons de représenter un même ensemble
de valeurs numériques.
Pourquoi de nombreux objets naturels sont-ils fractals ? Il semblerait qu'une réponse possible (la
réponse ?) vienne de cette "cohabitation" du fini et de l'infini qu'ils permettent.
A titre d'exemple,
les poumons, situés à l'intérieur du volume réduit de la cage thoracique,
assurent ainsi des échanges gazeux
(nous aurons l'occasion d'en présenter des images ultérieurement...)
sur une surface supérieure à cent mètres carrés
alors qu'une géométrie plus euclidienne (une sphère par exemple) donnerait un
dispositif gigantesque, instable et non viable !
3.3-Les Systèmes de Particules :
Dans toute expérience virtuelle les modèles mathématiques ne sont pas seuls à jouer
un role fondamental ; les programmes qui les rendent intelligibles aux ordinateurs
sont tout aussi importants.
Au dix-neuvième siècle, Heinrich Hertz déclarait de façon prophétique :
on ne peut échapper au sentiment que ces formules mathématiques
ont une existence qui leur est propre, qu'elles sont plus savantes que
ceux qui les ont découvertes, et que nous pouvons en extraire plus de science
qu'il n'en a été mis à l'origine. Cela est encore plus vrai aujourd'hui et peut s'étendre,
de plus, en substituant le mot programme
à l'expression formule mathématique.
A condition de suivre certains précepts de généralité
(Jacques Hadamard ne disait-il pas, en parlant alors des Mathématiques,
généraliser pour simplifier ?)
lors de la rédaction
des programmes, il sera possible de considérer chacun de ceux-ci
comme des expériences potentielles, c'est-à-dire
comme contenant potentiellement une infinité d'expériences sur un "thème donné".
Il convient de noter que dans l'univers de la création artistique,
le concept similaire d'œuvre potentielle pourra être défini avec le plus grand profit
[Plus d'informations...].
Illustrons ceci à l'aide d'un programme destiné à étudier l'évolution au cours du temps
d'ensembles de particules possédant diverses propriétés (taille, masse, charges diverses,
dureté, couleur...) interagissant éventuellement entre-elles et avec un milieu de géométrie
quelconque :
-
 Marche aléatoire isotrope de 4 particules sur un réseau carré bidimensionnel avec visualisation de leur centre de gravité -particule blanche-. Les six expériences qui vont suivre constituent l'ossature d'un
film pédagogique portant sur la Loi des Grands Nombres.
Dans ce premier cas, avec peu de particules, le système global est difficile
à prévoir, ce que le déplacement erratique du centre
de gravité montre parfaitement bien. Que se passe-t-il avec
beaucoup plus de particules ?
Marche aléatoire isotrope de 4 particules sur un réseau carré bidimensionnel avec visualisation de leur centre de gravité -particule blanche-. Les six expériences qui vont suivre constituent l'ossature d'un
film pédagogique portant sur la Loi des Grands Nombres.
Dans ce premier cas, avec peu de particules, le système global est difficile
à prévoir, ce que le déplacement erratique du centre
de gravité montre parfaitement bien. Que se passe-t-il avec
beaucoup plus de particules ?
-
 Marche aléatoire isotrope de 256 particules sur un réseau carré bidimensionnel avec visualisation de leur centre de gravité -particule blanche-. Avec beaucoup de particules, le système global est
est beaucoup plus facile à prévoir, ce que
la quasi-immobilité du centre de gravité montre.
Que se passe-t-il en remplaçant la marche aléatoire
sur réseau carré par des déplacements libres dans un billiard avec collisions ?
Marche aléatoire isotrope de 256 particules sur un réseau carré bidimensionnel avec visualisation de leur centre de gravité -particule blanche-. Avec beaucoup de particules, le système global est
est beaucoup plus facile à prévoir, ce que
la quasi-immobilité du centre de gravité montre.
Que se passe-t-il en remplaçant la marche aléatoire
sur réseau carré par des déplacements libres dans un billiard avec collisions ?
-
 Billard bidimensionnel rectangulaire avec 4 particules aléatoires en collision et visualisation de leur centre de gravité -particule blanche-. Le système est difficile à prévoir, comme pour la
marche aléatoire sur réseau carré.
Billard bidimensionnel rectangulaire avec 4 particules aléatoires en collision et visualisation de leur centre de gravité -particule blanche-. Le système est difficile à prévoir, comme pour la
marche aléatoire sur réseau carré.
-
 Billard bidimensionnel rectangulaire avec 256 particules aléatoires en collision et visualisation de leur centre de gravité -particule blanche-. Le système est facile à prévoir, comme pour la
marche aléatoire sur réseau carré. Que se passe-t-il
avec un billiard de forme plus complexe ?
Billard bidimensionnel rectangulaire avec 256 particules aléatoires en collision et visualisation de leur centre de gravité -particule blanche-. Le système est facile à prévoir, comme pour la
marche aléatoire sur réseau carré. Que se passe-t-il
avec un billiard de forme plus complexe ?
-
 Billard bidimensionnel de Sierpinski avec 4 particules aléatoires en collision et visualisation de leur centre de gravité -particule blanche-. Les résultats précédents semblent indépendants
de la forme du billiard.
Billard bidimensionnel de Sierpinski avec 4 particules aléatoires en collision et visualisation de leur centre de gravité -particule blanche-. Les résultats précédents semblent indépendants
de la forme du billiard.
-
 Billard bidimensionnel de Sierpinski avec 256 particules aléatoires en collision et visualisation de leur centre de gravité -particule blanche-. De même ici...
Billard bidimensionnel de Sierpinski avec 256 particules aléatoires en collision et visualisation de leur centre de gravité -particule blanche-. De même ici...
-
 Diffusion entre deux boîtes (conditions initiales : la boîte de gauche est vide alors que la boîte de droite contient 256 particules), avec collisions et une géométrie variable. Examinons maintenant une application à la thermodynamique.
Deux enceintes bidimensionnelles (l'une vide à gauche et l'autre pleine à droite)
communiquent par l'intermédiaire d'un orifice de diamètre
variable. Les pressions à l'intérieur des deux enceintes
s'équilibrent lentement en présence d'un faible diamètre et rapidement
avec un grand diamètre. Il convient de remarquer que, même si
la bidimensionnalité du système est peu physique, elle présente
l'avantage de produire des images plus "faciles à lire". Cette facilité
sera souvent exploitée dans un but pédagogique.
Diffusion entre deux boîtes (conditions initiales : la boîte de gauche est vide alors que la boîte de droite contient 256 particules), avec collisions et une géométrie variable. Examinons maintenant une application à la thermodynamique.
Deux enceintes bidimensionnelles (l'une vide à gauche et l'autre pleine à droite)
communiquent par l'intermédiaire d'un orifice de diamètre
variable. Les pressions à l'intérieur des deux enceintes
s'équilibrent lentement en présence d'un faible diamètre et rapidement
avec un grand diamètre. Il convient de remarquer que, même si
la bidimensionnalité du système est peu physique, elle présente
l'avantage de produire des images plus "faciles à lire". Cette facilité
sera souvent exploitée dans un but pédagogique.
-
 Front fractal de diffusion dans un milieu bidimensionnel obtenu grâce à des particules identiques en interaction. La diffusion est un phénomène naturel fondamental.
Ici, deux familles de particules strictement
identiques (l'une rouge et l'autre bleue, cette différence de couleur
ne correspondant à aucune propriété pouvant affecter le comportement
des particules) sont initialement
separées l'une de l'autre. Rapidement, elles
diffusent l'une dans l'autre et la frontière entre les deux
familles devient rapidement fractale.
Front fractal de diffusion dans un milieu bidimensionnel obtenu grâce à des particules identiques en interaction. La diffusion est un phénomène naturel fondamental.
Ici, deux familles de particules strictement
identiques (l'une rouge et l'autre bleue, cette différence de couleur
ne correspondant à aucune propriété pouvant affecter le comportement
des particules) sont initialement
separées l'une de l'autre. Rapidement, elles
diffusent l'une dans l'autre et la frontière entre les deux
familles devient rapidement fractale.
-
 L'effet domino bidimensionnel. Par le respect des lois fondamentales de conservation,
toutes les particules sont finalement mises en mouvement
à la suite d'un simple choc sur une unique particule centrale.
L'effet domino bidimensionnel. Par le respect des lois fondamentales de conservation,
toutes les particules sont finalement mises en mouvement
à la suite d'un simple choc sur une unique particule centrale.
-
 Mouvement brownien de quelques particules lourdes dans un gaz de particules légères et rapides.
Mouvement brownien de quelques particules lourdes dans un gaz de particules légères et rapides.
-
 Mouvement brownien de quelques particules lourdes et lumineuses dans un gaz de particules légères et rapides, avec un rapport croissant des rapports de masse (lourdes/légères=1,10,100,1000). Plus les sept particules lumineuses sont lourdes, plus leur mise
en mouvement est difficile...
Mouvement brownien de quelques particules lourdes et lumineuses dans un gaz de particules légères et rapides, avec un rapport croissant des rapports de masse (lourdes/légères=1,10,100,1000). Plus les sept particules lumineuses sont lourdes, plus leur mise
en mouvement est difficile...
-
 Particules en collision sans perte d'énergie dans un espace bidimensionnel avec visualisation de l'histogramme des modules des vitesses. Les conditions initiales choisies ne sont pas "physiques"
(les particules sont alors sur un réseau carré alors que leurs vitesses
sont les mêmes en module et aléatoires en direction).
Malgré cela, très rapidement, l'équilibre
thermodynamique est atteint grâce à des chocs parfaitement
élastiques, ce que montre l'enveloppe de
l'histogramme de distribution des modules des vecteurs vitesse en x.exp(-(x.x))
dans cette simulation bidimensionnelle.
Particules en collision sans perte d'énergie dans un espace bidimensionnel avec visualisation de l'histogramme des modules des vitesses. Les conditions initiales choisies ne sont pas "physiques"
(les particules sont alors sur un réseau carré alors que leurs vitesses
sont les mêmes en module et aléatoires en direction).
Malgré cela, très rapidement, l'équilibre
thermodynamique est atteint grâce à des chocs parfaitement
élastiques, ce que montre l'enveloppe de
l'histogramme de distribution des modules des vecteurs vitesse en x.exp(-(x.x))
dans cette simulation bidimensionnelle.
-
 Particules en collision sans perte d'énergie dans un espace tridimensionnel avec visualisation de l'histogramme des modules des vitesses. Dans le cas tridimensionnel, le comportement
est le même (l'enveloppe de l'histogramme de distribution
des modules des vecteurs vitesse étant cette fois en (x.x).exp(-(x.x))).
Particules en collision sans perte d'énergie dans un espace tridimensionnel avec visualisation de l'histogramme des modules des vitesses. Dans le cas tridimensionnel, le comportement
est le même (l'enveloppe de l'histogramme de distribution
des modules des vecteurs vitesse étant cette fois en (x.x).exp(-(x.x))).
-
 Détente d'un gaz dans une boîte circulaire bidimensionnelle avec visualisation de l'histogramme des modules des vitesses. Dans cet exemple, un gaz bidimensionnel est
à l'intérieur d'une enceinte circulaire de volume croissant
sans apport d'énergie. L'enveloppe de l'histogramme de
distribution des modules des vecteurs vitesse se conservant au cours du temps,
cette détente est donc isotherme.
Détente d'un gaz dans une boîte circulaire bidimensionnelle avec visualisation de l'histogramme des modules des vitesses. Dans cet exemple, un gaz bidimensionnel est
à l'intérieur d'une enceinte circulaire de volume croissant
sans apport d'énergie. L'enveloppe de l'histogramme de
distribution des modules des vecteurs vitesse se conservant au cours du temps,
cette détente est donc isotherme.
-
 Billard bidimensionnel de Sierpinski avec 326 particules isotropes soumises à un fort champ de gravitation vertical. Un gaz bidimensionnel est à l'intérieur d'une enceinte
de forme complexe et est soumis à un fort potentiel
gravitationnel "vertical". Les particules sont donc entrainées
vers le bas ; malgré cela, un gradient vertical de densité
apparait dû à la pression élevée régnant dans les compartiments
inférieurs.
Billard bidimensionnel de Sierpinski avec 326 particules isotropes soumises à un fort champ de gravitation vertical. Un gaz bidimensionnel est à l'intérieur d'une enceinte
de forme complexe et est soumis à un fort potentiel
gravitationnel "vertical". Les particules sont donc entrainées
vers le bas ; malgré cela, un gradient vertical de densité
apparait dû à la pression élevée régnant dans les compartiments
inférieurs.
-
 Un piston bidimensionnel parfait avec les conditions initiales suivantes : piston immobîle, particules chaudes à gauche et froides à droite, le tout dans une boîte bidimensionnelle soumise à un champ de gravitation vertical. Un piston bidimensionnel parfait (sans frottement) à l'intérieur d'une
boîte bidimensionnelle immergée dans un fort potentiel gravitationnel "vertical".
A sa gauche se trouve un gaz chaud (de couleur rouge),
tandis qu'a sa droite se trouve un gaz froid (de couleur verte).
Le gaz chaud se détend et comprime le gaz froid ; le piston
subit ensuite des oscillations amorties. Enfin, le gaz froid se solidifie
selon un réseau cristallin hexagonal, alors qu'à gauche
les trois phases solide, liquide et gazeuse peuvent être
observées.
Un piston bidimensionnel parfait avec les conditions initiales suivantes : piston immobîle, particules chaudes à gauche et froides à droite, le tout dans une boîte bidimensionnelle soumise à un champ de gravitation vertical. Un piston bidimensionnel parfait (sans frottement) à l'intérieur d'une
boîte bidimensionnelle immergée dans un fort potentiel gravitationnel "vertical".
A sa gauche se trouve un gaz chaud (de couleur rouge),
tandis qu'a sa droite se trouve un gaz froid (de couleur verte).
Le gaz chaud se détend et comprime le gaz froid ; le piston
subit ensuite des oscillations amorties. Enfin, le gaz froid se solidifie
selon un réseau cristallin hexagonal, alors qu'à gauche
les trois phases solide, liquide et gazeuse peuvent être
observées.
-
 Un fluide bidimensionnel périodique avec des vitesses strictement identiques initialement et un obstacle central très légèrement décale verticalement, avec visualisation de l'histogramme des modules des vitesses. Passage rapide de l'ordre parfait au désordre
grâce à un obstacle central immobile (blanc) légèrement décalé verticalement,
introduisant ainsi une légère dissymétrie lors des premiers chocs qu'il subit.
Celui-ci gène la progression d'un fluide de particules
strictement identiques initialement (tous les vecteurs vitesse sont égaux
-même module et même direction horizontale-).
Un fluide bidimensionnel périodique avec des vitesses strictement identiques initialement et un obstacle central très légèrement décale verticalement, avec visualisation de l'histogramme des modules des vitesses. Passage rapide de l'ordre parfait au désordre
grâce à un obstacle central immobile (blanc) légèrement décalé verticalement,
introduisant ainsi une légère dissymétrie lors des premiers chocs qu'il subit.
Celui-ci gène la progression d'un fluide de particules
strictement identiques initialement (tous les vecteurs vitesse sont égaux
-même module et même direction horizontale-).
-
 Agrégats fractals bidimensionnels obtenus par collage de 100% des particules lors de leurs collisions, dans un champ de gravitation central attractif. Dans tous les exemples précédents, les chocs
étaient parfaitement élastiques. Dans le cas présent,
les particules, lors d'une collision, se
collent les unes aux autres. Par l'intermédiaire d'un potentiel
gravitationnel dit central
(c'est-à-dire dont la source est située au centre de la boite rectangulaire
contenant les particules), des agrégats de plus un plus importants
se constituent. A la fin l'objet obtenu est un agrégat fractal
très filamenteux. Que se passerait-il si toutes les particules
ne se collaient pas les unes aux autres ?
Agrégats fractals bidimensionnels obtenus par collage de 100% des particules lors de leurs collisions, dans un champ de gravitation central attractif. Dans tous les exemples précédents, les chocs
étaient parfaitement élastiques. Dans le cas présent,
les particules, lors d'une collision, se
collent les unes aux autres. Par l'intermédiaire d'un potentiel
gravitationnel dit central
(c'est-à-dire dont la source est située au centre de la boite rectangulaire
contenant les particules), des agrégats de plus un plus importants
se constituent. A la fin l'objet obtenu est un agrégat fractal
très filamenteux. Que se passerait-il si toutes les particules
ne se collaient pas les unes aux autres ?
-
 Agrégats fractals bidimensionnels obtenus par collage de 50% des particules lors de leurs collisions, dans un champ de gravitation central attractif. Lorsque seulement une partie des particules sont "collantes"
(50% dans cet exemple), ces particules continuent
à former un agrégat fractal (de couleur blanche) qui peut sembler
plus trapu car il piège en fait de nombreuses particules non collantes.
Agrégats fractals bidimensionnels obtenus par collage de 50% des particules lors de leurs collisions, dans un champ de gravitation central attractif. Lorsque seulement une partie des particules sont "collantes"
(50% dans cet exemple), ces particules continuent
à former un agrégat fractal (de couleur blanche) qui peut sembler
plus trapu car il piège en fait de nombreuses particules non collantes.
-
 Agrégats fractals bidimensionnels obtenus par collage de 100% des particules lors de leurs collisions, dans un champ de gravitation vertical. Refaisons l'expérience avec 100% de particules collantes
et un potentiel gravitationnel "vertical".
Agrégats fractals bidimensionnels obtenus par collage de 100% des particules lors de leurs collisions, dans un champ de gravitation vertical. Refaisons l'expérience avec 100% de particules collantes
et un potentiel gravitationnel "vertical".
-
 Agrégats fractals bidimensionnels obtenus par collage de 50% des particules lors de leurs collisions, dans un champ de gravitation vertical. Refaisons l'experience avec 50% de particules collantes
et un potentiel gravitationnel "vertical".
Que se passe-t-il si toutes ces expériences
étaient effectuées dans un espace tridimensionnel ?
Agrégats fractals bidimensionnels obtenus par collage de 50% des particules lors de leurs collisions, dans un champ de gravitation vertical. Refaisons l'experience avec 50% de particules collantes
et un potentiel gravitationnel "vertical".
Que se passe-t-il si toutes ces expériences
étaient effectuées dans un espace tridimensionnel ?
-
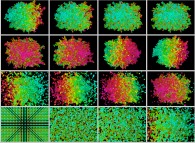 Agrégat fractal tridimensionnel obtenu par collage de 100% des particules lors de leurs collisions, dans un champ de gravitation central. Là-aussi, l'expérience aboutit à un agrégat
fractal, mais dont la forme est beaucoup plus difficile
à saisir car il réside dans un espace tridimensionnel ; une
rotation de cet "objet" sous les yeux de l'observateur est donc introduite afin d'en
faciliter la compréhension.
Agrégat fractal tridimensionnel obtenu par collage de 100% des particules lors de leurs collisions, dans un champ de gravitation central. Là-aussi, l'expérience aboutit à un agrégat
fractal, mais dont la forme est beaucoup plus difficile
à saisir car il réside dans un espace tridimensionnel ; une
rotation de cet "objet" sous les yeux de l'observateur est donc introduite afin d'en
faciliter la compréhension.
-
 Agrégat fractal tridimensionnel obtenu par collage de 50% des particules lors de leurs collisions, dans un champ de gravitation central.
Agrégat fractal tridimensionnel obtenu par collage de 50% des particules lors de leurs collisions, dans un champ de gravitation central.
-
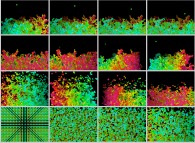 Agrégats fractals tridimensionnels obtenus par collage de 100% des particules lors de leurs collisions, dans un champ de gravitation vertical.
Agrégats fractals tridimensionnels obtenus par collage de 100% des particules lors de leurs collisions, dans un champ de gravitation vertical.
-
 Agrégats fractals tridimensionnels obtenus par collage de 50% des particules lors de leurs collisions, dans un champ de gravitation vertical.
Agrégats fractals tridimensionnels obtenus par collage de 50% des particules lors de leurs collisions, dans un champ de gravitation vertical.
-
 La marche aléatoire des photons produits au cœur du Soleil. La lumière qui éclaire et réchauffe notre Terre
est produite par des réactions nucléaires au cœur du Soleil.
Huit minutes lui suffisent pour nous arriver. Mais, par contre,
pour sortir du Soleil, chaque photon est l'objet d'une marche
aléatoire d'une durée moyenne de 100.000 ans ! Il convient d'une part de noter
que la sortie de chacun d'eux se fait selon une direction arbitraire
relativement au vecteur normal ; c'est cela qui explique la luminosité
uniforme du disque solaire (il n'apparait pas comme une sphère...).
D'autre part, cette expérience est un exemple caractéristique
d'une difficulté rencontrée fréquemment lors de la visualisation de
systèmes physiques : l'impossibilité de respecter les échelles
spatiales et/ou temporelles...
La marche aléatoire des photons produits au cœur du Soleil. La lumière qui éclaire et réchauffe notre Terre
est produite par des réactions nucléaires au cœur du Soleil.
Huit minutes lui suffisent pour nous arriver. Mais, par contre,
pour sortir du Soleil, chaque photon est l'objet d'une marche
aléatoire d'une durée moyenne de 100.000 ans ! Il convient d'une part de noter
que la sortie de chacun d'eux se fait selon une direction arbitraire
relativement au vecteur normal ; c'est cela qui explique la luminosité
uniforme du disque solaire (il n'apparait pas comme une sphère...).
D'autre part, cette expérience est un exemple caractéristique
d'une difficulté rencontrée fréquemment lors de la visualisation de
systèmes physiques : l'impossibilité de respecter les échelles
spatiales et/ou temporelles...
-
 Diffusion de particules à l'intérieur du modèle de l'acinus pulmonaire humain dû à Hiroko Kitaoka. Les poumons forment une structure fractale assurant les
échanges gazeux entre l'air et le sang. Ces expériences montrent
la diffusion des gaz dans les alvéoles
(ou acinus pulmonaire). Ici les particules
blanches situées à l'origine de l'arborescence diffusent mieux
que les particules colorées car ces dernières sont situées (et donc
"piégées") aux extrémités.
Diffusion de particules à l'intérieur du modèle de l'acinus pulmonaire humain dû à Hiroko Kitaoka. Les poumons forment une structure fractale assurant les
échanges gazeux entre l'air et le sang. Ces expériences montrent
la diffusion des gaz dans les alvéoles
(ou acinus pulmonaire). Ici les particules
blanches situées à l'origine de l'arborescence diffusent mieux
que les particules colorées car ces dernières sont situées (et donc
"piégées") aux extrémités.
-
 Diffusion de particules à l'intérieur du modèle de l'acinus pulmonaire humain dû à Hiroko Kitaoka avec perméabilité de la membrane. Le mélange gazeux est composé approximativement de 80% d'azote et de 20%
d'oxygène. La densité de ce dernier décroit en s'éloignant
de l'origine de l'arborescence. L'une des difficultés rencontrées
lors de ces expériences virtuelles résident dans la complexité
de la géométrie du système. Que faire donc pour en faciliter la
compréhension ? La solution adoptée ici consiste à faire tourner
le système sous les yeux de l'observateur.
Diffusion de particules à l'intérieur du modèle de l'acinus pulmonaire humain dû à Hiroko Kitaoka avec perméabilité de la membrane. Le mélange gazeux est composé approximativement de 80% d'azote et de 20%
d'oxygène. La densité de ce dernier décroit en s'éloignant
de l'origine de l'arborescence. L'une des difficultés rencontrées
lors de ces expériences virtuelles résident dans la complexité
de la géométrie du système. Que faire donc pour en faciliter la
compréhension ? La solution adoptée ici consiste à faire tourner
le système sous les yeux de l'observateur.
-
 Diffusion de particules à l'intérieur du modèle de l'acinus pulmonaire humain dû à Hiroko Kitaoka avec perméabilité de la membrane. Pour faciliter la compréhension de la géométrie de ce système,
une autre solution consiste à le déplier et à le mettre à plat
tout en conservant, évidemment, la tridimensionnalité de ses conduits.
Diffusion de particules à l'intérieur du modèle de l'acinus pulmonaire humain dû à Hiroko Kitaoka avec perméabilité de la membrane. Pour faciliter la compréhension de la géométrie de ce système,
une autre solution consiste à le déplier et à le mettre à plat
tout en conservant, évidemment, la tridimensionnalité de ses conduits.
3.4-La Mécanique Céleste :
Le sens de la vision, toujours en alerte, pourra réagir instantanément
à toute surprise visuelle apparaissant durant une expérience virtuelle et ainsi,
de cette nouvelle approche pourront surgir des découvertes éventuellement importantes.
-
 Visualisation de l'inclinaison de deux trajectoires elliptiques. Cette expérience à caractère didactique est destinée à montrer
la notion d'inclinaison. Dans ce système à trois corps,
deux planètes orbitent autour d'une étoile dans des plans différents.
Au cours du mouvement de l'observateur autour du système, il est
possible de voir la ligne des nœuds (ligne
d'intersection des plans de deux trajectoires qui passe évidemment par leur
foyer commun).
Visualisation de l'inclinaison de deux trajectoires elliptiques. Cette expérience à caractère didactique est destinée à montrer
la notion d'inclinaison. Dans ce système à trois corps,
deux planètes orbitent autour d'une étoile dans des plans différents.
Au cours du mouvement de l'observateur autour du système, il est
possible de voir la ligne des nœuds (ligne
d'intersection des plans de deux trajectoires qui passe évidemment par leur
foyer commun).
-
 Intégration du problème des N-corps (N=10) montrant le véritable système solaire avec une rotation simultanée de 2.pi. En injectant dans le modèle du problème des N-corps
les coordonnées et les vitesses des neuf planètes connues (a la date du 26/10/2002)
du système solaire
à une date donnée, il est possible de calculer leurs trajectoires ultérieures.
Au cours de cette expérience, l'observateur tourne autour du
système afin de bien noter le cas particulier de Pluton dont la
trajectoire n'est pas dans le plan des autres planètes (dit
plan de l'écliptique). Il est important de noter
l'aspect "mensonger" de cette représentation. En effet, le
système solaire ne peut être représenté à l'échelle ; le Soleil,
dans ce cas, serait plus petit qu'un point d'image et son
diamètre doit donc être démesurément exagéré. De même, les planètes apparaissent
comme ayant une taille du même ordre de grandeur que celle du Soleil, ce qui n'est
évidemment pas le cas en réalité. Enfin, étant donné le diamètre
de la sphère matérialisant le Soleil, les trajectoires des quatre
premières planètes devraient être cachées par celle-ci. Ainsi, il est nécessaire,
après des calculs respectant les échelles réelles, de procéder
à des dilatations non linéaires des trajectoires de façon à pouvoir
les distinguer.
Intégration du problème des N-corps (N=10) montrant le véritable système solaire avec une rotation simultanée de 2.pi. En injectant dans le modèle du problème des N-corps
les coordonnées et les vitesses des neuf planètes connues (a la date du 26/10/2002)
du système solaire
à une date donnée, il est possible de calculer leurs trajectoires ultérieures.
Au cours de cette expérience, l'observateur tourne autour du
système afin de bien noter le cas particulier de Pluton dont la
trajectoire n'est pas dans le plan des autres planètes (dit
plan de l'écliptique). Il est important de noter
l'aspect "mensonger" de cette représentation. En effet, le
système solaire ne peut être représenté à l'échelle ; le Soleil,
dans ce cas, serait plus petit qu'un point d'image et son
diamètre doit donc être démesurément exagéré. De même, les planètes apparaissent
comme ayant une taille du même ordre de grandeur que celle du Soleil, ce qui n'est
évidemment pas le cas en réalité. Enfin, étant donné le diamètre
de la sphère matérialisant le Soleil, les trajectoires des quatre
premières planètes devraient être cachées par celle-ci. Ainsi, il est nécessaire,
après des calculs respectant les échelles réelles, de procéder
à des dilatations non linéaires des trajectoires de façon à pouvoir
les distinguer.
-
 Intégration du problème des N-corps (N=10) montrant le véritable système solaire avec une rotation simultanée de 2.pi, notre Terre étant choisie comme origine des coordonnées. Quel est le ciel que voyaient nos ancêtres et que nous voyons
encore en le regardant "naïvement". Cette expérience place donc la
Terre au centre du système solaire (par un simple changement de référentiel).
Le Soleil tourne alors autour de
la Terre, alors que les huit autres planètes décrivent des
boucles de rétrogradation qui furent longtemps expliquées à grand
coup d'épicycles (du moins jusqu'à Copernic...).
Intégration du problème des N-corps (N=10) montrant le véritable système solaire avec une rotation simultanée de 2.pi, notre Terre étant choisie comme origine des coordonnées. Quel est le ciel que voyaient nos ancêtres et que nous voyons
encore en le regardant "naïvement". Cette expérience place donc la
Terre au centre du système solaire (par un simple changement de référentiel).
Le Soleil tourne alors autour de
la Terre, alors que les huit autres planètes décrivent des
boucles de rétrogradation qui furent longtemps expliquées à grand
coup d'épicycles (du moins jusqu'à Copernic...).
-
 De Pluton au Soleil (échelles non linéaires). Alors comment serait perçu notre système solaire depuis
un point de vue quelconque ? C'est ce que montre cette expérience
dans laquelle une dixième planète n'interagissant pas avec les
autres (mais uniquement avec le Soleil) et dont quelques trajectoires possibles sont étudiées
depuis l'orbite de Pluton jusqu'au voisinage du Soleil. Le ciel perçu par ses habitants
(virtuels) serait très régulier à proximit/ du Soleil et progressivement
deviendrait d'une telle complexité qu'aucun système d'épicycles
ne saurait l'expliquer. La leçon à tirer de cela est double : d'une
part un système peut présenter un "visage" complexe, voire
chaotique, alors qu'en fait, à condition de trouver
le bon point de vue, il peut se simplifier considérablement (mais
comment trouver le "bon point de vue" pour un système quelconque ?).
Ce phénomene nous permet d'introduire la notion de
Chaos Virtuel ou Subjectif
[Plus d'informations...].
D'autre part, si notre humanité s'était developpée plus loin
du Soleil et en dehors du plan de l'écliptique (si tant est que la
chose fut possible), nos astronomes, nos mathématiciens,
mais aussi nos prêtres des temps passés auraient observé un ciel beaucoup
plus irrégulier ; les conséquences en auraient été certainement considérables en ce qui
concerne la science, la philosophie et certainement les religions...
De Pluton au Soleil (échelles non linéaires). Alors comment serait perçu notre système solaire depuis
un point de vue quelconque ? C'est ce que montre cette expérience
dans laquelle une dixième planète n'interagissant pas avec les
autres (mais uniquement avec le Soleil) et dont quelques trajectoires possibles sont étudiées
depuis l'orbite de Pluton jusqu'au voisinage du Soleil. Le ciel perçu par ses habitants
(virtuels) serait très régulier à proximit/ du Soleil et progressivement
deviendrait d'une telle complexité qu'aucun système d'épicycles
ne saurait l'expliquer. La leçon à tirer de cela est double : d'une
part un système peut présenter un "visage" complexe, voire
chaotique, alors qu'en fait, à condition de trouver
le bon point de vue, il peut se simplifier considérablement (mais
comment trouver le "bon point de vue" pour un système quelconque ?).
Ce phénomene nous permet d'introduire la notion de
Chaos Virtuel ou Subjectif
[Plus d'informations...].
D'autre part, si notre humanité s'était developpée plus loin
du Soleil et en dehors du plan de l'écliptique (si tant est que la
chose fut possible), nos astronomes, nos mathématiciens,
mais aussi nos prêtres des temps passés auraient observé un ciel beaucoup
plus irrégulier ; les conséquences en auraient été certainement considérables en ce qui
concerne la science, la philosophie et certainement les religions...
-
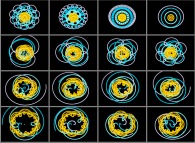 Simulation de 'de Pluton au Soleil' avec de purs mouvements circulaires uniformes (échelles linéaires). Notons au passage que ce Chaos Virtuel (ou Subjectif) n'est pas lié au caractère
approximativement elliptique des trajectoires, mais uniquement
à la notion de mouvement relatif ainsi que l'illustre cette expérience
qui n'utilise que des mouvements circulaires concentriques et uniformes
(ou encore plus simplement lors de l'observation de la pluie qui tombe...).
Simulation de 'de Pluton au Soleil' avec de purs mouvements circulaires uniformes (échelles linéaires). Notons au passage que ce Chaos Virtuel (ou Subjectif) n'est pas lié au caractère
approximativement elliptique des trajectoires, mais uniquement
à la notion de mouvement relatif ainsi que l'illustre cette expérience
qui n'utilise que des mouvements circulaires concentriques et uniformes
(ou encore plus simplement lors de l'observation de la pluie qui tombe...).
-
 De Pluton au Soleil -extrapolation 1- (échelles non linéaires). Enfin, dans cette dernière expérience, la planète
fictive conserve une trajectoire de taille fixe, mais son
plan tourne de 360 degrés dans l'espace.
De Pluton au Soleil -extrapolation 1- (échelles non linéaires). Enfin, dans cette dernière expérience, la planète
fictive conserve une trajectoire de taille fixe, mais son
plan tourne de 360 degrés dans l'espace.
4-LES DIFFICULTES ET LES LIMITES DE L'OUTIL :
Les quelques exemples précédents d'expériences virtuelles
pourraient laisser croire que la situation est idyllique...
En fait, il n'en est rien.
Au préalable, il convient de rappeler que lors
d'une expérience virtuelle nous ne faisons qu'étudier le
modèle d'un système et non point ce système lui-même.
Confondre le système et son modèle serait identique à ne pas faire de différence entre un
paysage et sa photographie. Le modèle ne peut pas,
sauf cas très particuliers, représenter le système
dans toute sa complexité. Les approches "réelle" et "virtuelle"
sont bien évidemment complémentaires et les prédictions faites grâce aux
Mathématiques et à la Programmation, lorsqu'elles
concernent des "fragments" de Réalité, doivent être
validées (précisons qu'il est aussi possible de faire des
expériences virtuelles dans des univers purement imaginaires, auquel cas ce risque de
confusion ne se rencontre pas).
Tout reposant finalement sur l'ordinateur,
la programmation sous-jacente
conditionnera bien entendu (mais qui s'en souvient ?) la qualité, la
valeur et la cohérence des résultats
scientifiques obtenus. Mais une
programmation exempte d'erreurs (sachant
que, en dehors d'exemples simplistes, elle
n'existe malheureusement pas...) est-elle
garante de cette qualité ? Nous allons
montrer qu'il n'en est rien. Trois raisons
vont se conjuguer pour rendre parfois
douteux nos résultats ; en effet,
contrairement peut-être à certaines idées
préconçues, il est difficile d'une part de
calculer à l'aide d'un ordinateur, d'autre part
de visualiser des résultats numériques et
enfin de résister à la tentation de faire des
images spectaculaires sans intérêt
scientifique (ou pédagogique)...
4.1-Les Développements Mathématiques :
Il est évident qu'au niveau de l'analyse mathématique du problème
de nombreuses erreurs peuvent apparaître : de nature conceptuelle,
d'utilisation d'hypothèses implicites, de mise en place d'un
contexte inapproprié (par exemple, oublier les phénomènes relativistes
en présence de vitesses importantes),...,
et plus "bêtement", de vulgaires fautes de signes...
D'autre part, et c'est là un point essentiel
que nous détaillerons ci-apres,
il convient de garder présent à l'esprit en permanence
qu'un ordinateur est une machine tout à la fois finie et discrète.
Cela signifie que, sauf cas très exceptionnels,
le modèle mathématique ne peut être
utilisé tel quel ; il est impératif de lui appliquer des méthodes
dites numériques afin que des résultats
concrets puissent être obtenus. Cela signifie, par exemple,
que le temps et l'espace doivent être échantillonnés et représentés ainsi
par un ensemble fini de points. Ce processus est évidemment source
d'anomalies graves.
Une fois ces deux premières étapes franchies (analyses mathématique et numérique respectivement),
le modèle est théoriquement
prêt à être mis en œuvre dans un ordinateur...
4.2-La Programmation :
S'il peut apparaître évident à beaucoup qu'il est bien plus facile de
rédiger un programme qui fonctionne mal qu'un programme au comportement parfait,
cela est malheureusement bien souvent oublié ; il est vrai d'ailleurs que les outils
mis à notre disposition (tant au niveau logiciel qu'au niveau matériel) donnent l'illusion
d'une grande (trop grande ?) facilité...
S'il l'ordinateur peut aisément indiquer au programmeur qu'une parenthèse
ouvrante n'est associée à aucune parenthèse fermante, ou encore qu'une
suite d'opérateurs n'a aucun sens, hors de l'aspect syntaxique des programmes
l'ordinateur n'a que peu de compétences. En effet, par exemple,
comment pourrait-il deviner que le 'A+B' que le programmeur a écrit aurait du
être en fait un 'A-B' par rapport au problème posé ?
Certains utopistes fondent de grands espoirs sur une approche de la programmation
de beaucoup plus haut niveau, ou le programmeur ne ferait que spécifier
son problème, laissant le soin à "quelque chose" de programmer à sa place.
Deux remarques s'imposent alors : d'une part, les spécifications d'un problème
complexe sont en général elles-mêmes complexes et peuvent donc contenir des erreurs, des
incohérences,... D'autre part, ce "quelque chose" est nécessairement un
programme, lui-même d'une grande complexité et donc victime potentielle des
mêmes maux que les autres programmes... Notons au passage que le nombre d'erreurs
contenues dans un programme croit exponentiellement avec la complexité de celui-ci ;
ainsi, au-delà d'un certain seuil, tout programme contient des anomalies,
celles-ci pouvant d'ailleurs ne jamais se manifester, ou bien se produire au bout
de nombreuses années d'utilisation sans problèmes apparents...
Imaginons malgré tout qu'un programme exempt de fautes ait été rédigé.
Evidemment cette hypothèse ne concerne que les fautes de logique,
puisque les fautes de syntaxe sont nécessairement détectées par l'ordinateur,
puis corrigées par le programmeur. Cela est possible : il suffit, par exemple,
de réaliser un programme simple et court (notons au passage que même dans ce cas,
le programmeur pourrait avoir oublié quelques cas particuliers : l'expérience
peut être tentée en proposant à quelqu'un de programmer la simple résolution de
l'équation du second degré...).
Malgré cette perfection, le programme produira-t-il les résultats attendus ?
Malheureusement cela n'est pas toujours le cas pour une première raison liée
à la compilation, opération qui consiste à traduire un programme écrit en
langage de haut niveau (par exemple le Fortran) en une suite d'opérations élémentaires
(les quatre opérations de l'arithmétique, la comparaison de deux nombres,...)
que seules les processeurs savent exécuter.
Un compilateur est lui-même fait d'un ensemble de programmes complexes et même s'ils
sont en général bien testés (à cause, en particulier, de l'usage intensif
qui en est fait, sachant que, malgré tout, des tests exhaustifs
sont tout simplement impossibles), ils ne sont pas exempts d'erreurs (comme tout autre programme...).
Ainsi, par exemple,
avec la version 2.7.1 du compilateur
'gcc' sur DEC VAX sous ULTRIX, l'expression :
0
---
x
est interprétée comme :
1
-----
2.x
ce qui est mathématiquement peu correct !
Mais les compilateurs n'ont pas l'exclusivité des anomalies !
Les librairies utilisées (et dans lesquelles le programmeur pourra trouver,
par exemple, les fonctions mathématiques usuelles), elles-aussi, peuvent présenter
des comportements aberrants. Ainsi,
avec les versions 6.0.1 et 6.1 du système
IRIX Silicon Graphics,
il est impossible de faire confiance à la fonction 'pow(...)'
de la librairie 'libm43'. A titre d'exemple, le calcul
des premières puissances de 2 donne :
0
2 = 1
1
2 = 2
2
2 = 4
3
2 = 363031686155.84345
4
2 = -2194234532479271.8
ce qui constitue, à partir de la puissance
troisième, une approximation relativement
grossière de la valeur exacte !
Une remarque essentielle s'impose alors : pour quelques erreurs
détectées (parce que leurs conséquences étaient "visibles"),
combien d'erreurs latentes sont présentes ?
Ainsi, un programme peut-être correct au niveau de son source,
alors que son exécutable peut, sur un certain système,
ne pas l'être !
Par exemple, cette image  semble correspondre visuellement à ce qui est attendu du programme
géniteur, mais est-elle ce qu'elle serait si ce programme
(supposé sans erreurs de logique...) était exploité sur un système parfait ?
semble correspondre visuellement à ce qui est attendu du programme
géniteur, mais est-elle ce qu'elle serait si ce programme
(supposé sans erreurs de logique...) était exploité sur un système parfait ?
Il faut noter au passage que, malgré tout, il est possible
de développer des stratégies destinées à améliorer la situation
[Plus d'informations...]
Mais malheureusement l'histoire n'est pas terminée...
4.3-Le Calcul :
Finalement tout se ramène donc à des calculs effectués par des processeurs.
L'un des "objets fondamentaux" de la physique mathématique est le corps
des nombres réels [Plus d'informations...].
Or la précision des opérations
(exprimée en nombre de bits mémorisés et manipulés lors des calculs ;
aujourd'hui, le monde scientifique utilise majoritairement les représentations sur 64 bits)
est limitée pour des raisons théoriques (que faire d'autre ?),
pratiques et économiques évidentes.
Les nombres réels ne pourront donc pas , sauf cas particuliers,
être représentés exactement dans un ordinateur : ils n'existent tout simplement pas
pour ces machines !
Un ordinateur (quelqu'en soit le type) est une machine tout à la
fois finie (elle possède une capacité mémoire limitée) et
"discrète" (l'information doit être échantillonnée et quantifiée avant tout
traitement numérique). Ces deux caractéristiques sont malheureusement
trop souvent oubliées, ce qui peut être alors la source de
désagrements (euphémisme...).
A titre d'exemple du caractère fini
des ordinateurs, étudions la suite définie par :
S = 0
0
S = S + 1
n n-1
Quelle est donc la valeur de S(n) ? La réponse "mathématique"
est évidemment :
S = n
n
Malheureusement, la réponse "informatique" peut être très
différente, ainsi que le montre le programme suivant,
destiné à calculer numériquement cette valeur :
#define N "une certaine valeur positive et entière..."
main()
{
int n;
float sigma=0;
for (n=1 ; n <= N ; n++)
{
sigma = sigma + 1.0;
}
printf("\n somme calculee = %f",sigma);
}
Il donne systématiquement la valeur 16777216
(alors qu'il devrait évidemment donner la valeur N en l'absence de ce problème...)
pour toute valeur de N supérieure ou égale a 16777216.
En ce qui concerne le caractère discret
des ordinateurs, la conséquence immédiate est, en
toute généralité, l'impossibilité
de manipuler les nombres Réels. Ces derniers n'existent tout
simplement pas dans l'univers numérique. Ils sont très grossièrement
approchés par les nombres dits flottants.
A cause de cela, des constantes apparemment très simple (par exemple
4095.1 et 4096.1 qui seront utilisées ci-après)
ne sont pas représentables exactement en machine.
De plus, pour ces nombres, les opérations arithmétiques élémentaires
ne sont en général pas internes.
Lors de chacune d'entre-elles,
une erreur d'arrondi est introduite ;
celle-ci est alors la cause
de la perte de la propriété d'associativité
de l'addition et surtout
de celle de la multiplication (notons que dans ces conditions,
la multiplication n'est alors plus distributive par rapport a l'addition).
Ainsi, par exemple, en simple précision (c'est-à-dire sur 32 bits
et ce afin de simplifier l'impression hexa-décimale des résultats
-voir la même expérience en double précision 64 bits-),
le programme suivant (ou la fonction 'MUL' est destinée a forcer l'ordre
des multiplications) :
float MUL(x,y)
float x,y;
{
return(x*y);
}
main()
{
float A=3.1,B=2.3,C=1.5;
float X,Y;
X=MUL(MUL(A,B),C);
Y=MUL(A,MUL(B,C));
printf("\n (%f x %f) x %f = %f\n",A,B,C,X);
printf("\n %f x (%f x %f) = %f\n",A,B,C,Y);
}
donne comme résultats :
(3.10 * 2.30) * 1.50 = 10.695000 = 0x412B1EB8
#### #
et :
3.10 * (2.30 * 1.50) = 10.694999 = 0x412B1EB7
#### #
ce qui constitue deux résultats différents. On notera au passage,
que d'une part l'écriture de ce programme pourrait être bien plus
concise, mais que s'il est ainsi redigé, c'est
dans l'espoir de contrôler le plus possible le code généré par
le compilateur, aucune optimisation n'étant demandée
évidemment. D'autre part, l'expérience peut être refaite
avec d'autres langages de programmation (par exemple java
ou le programmeur maitrise l'ordre d'évaluation des opérations,
mais est-ce bien vrai ?) ;
elle produit évidemment le même phénomène...
L'expérience précédente pourrait être tentée à l'aide du programme :
main()
{
float A=3.1,B=2.3,C=1.5;
float X,Y;
X=(A*B)*C;
Y=A*(B*C);
printf("\n (%f x %f) x %f = %f",A,B,C,X);
printf("\n %f x (%f x %f) = %f",A,B,C,Y);
}
Lorsqu'elle ne montre pas le phénomène ici décrit,
deux explications, au moins, peuvent être avancées :
- le compilateur utilisé transforme la simple
simple précision 32 bits
en double précision 64 bits
à l'insu de l'utilisateur,
- le compilateur utilisé compile de façon similaire
les expressions (AxB)xC et Ax(BxC),
supposant la propriété d'associativité satisfaite.
Il conviendra alors d'augmenter le nombre de décimales
des trois variables 'A', 'B' et 'C', ou
encore d'essayer un autre compilateur, ou enfin
évidemment d'exploiter le programme utilisant la fonction 'MUL'...
Il convient de noter que la propriété d'associativité de l'addition
est donc, elle-aussi perdue, mais qu'elle se manifeste
plus rarement et de façon moins grave au niveau de ses consèquences.
Ainsi, par exemple, en simple précision (c'est-à-dire sur 32 bits
et ce afin de simplifier l'impression hexa-décimale des résultats
-voir la même expérience en double précision 64 bits-),
le programme suivant
(ou la fonction 'ADD' est destinée à forcer l'ordre des additions) :
float ADD(x,y)
float x,y;
{
return(x+y);
}
main()
{
float A=1.1,B=3.3,C=5.5;
float X,Y;
X=ADD(ADD(A,B),C);
Y=ADD(A,ADD(B,C));
printf("\n (%f x %f) x %f = %f\n",A,B,C,X);
printf("\n %f x (%f x %f) = %f\n",A,B,C,Y);
}
donne :
(1.10 + 3.30) + 5.50 = 9.900000 = 0x411E6666
# #
ce qui est différent de :
1.10 + (3.30 + 5.50) = 9.900001 = 0x411E6667
# #
[Evidemment une anomalie similaire peut-être constaté avec la distributivité de la multiplication sur l'addition]
Le seul aspect positif de ce "dysfonctionnement" est qu'il permet de
nous rappeler (montrer ?) qu'un ordinateur, sauf cas particuliers
(celui des petits nombres entiers, par exemple),
ne calcule pas exactement !
Lors de l'étude de problèmes non linéaires,
tout cela peut avoir des conséquences absolument
dévastatrices. A titre d'exemple, le calcul de l'itération
(dite Dynamique de Verhulst ) :
2
X = (R+1)X - RX
n n-1 n-1
qui est équivalent à la succession des calculs suivants :
X
0
|
---------------
| |
\|/ \|/
' '
2
X = (R+1)X - RX
1 0 0
|
---------------
| |
\|/ \|/
' '
2
X = (R+1)X - RX
2 1 1
|
---------------
| |
\|/ \|/
' '
2
X = (R+1)X - RX
3 2 2
|
---------------
| |
\|/ \|/
' '
etc...
peut se faire par le programme élémentaire, voire simpliste,
donné de façon très détaillée ci-après (sont mises en gras, les lignes
réellement essentielles) :
main()
{
double R=3.0;
double X=0.5;
int n;
for (n=0 ; n <= 80 ; n++)
{
if ((n%10) == 0)
{
printf("\n iteration(%04d) = %9.6f",n,X);
}
else
{
}
X = (R+1)*X - R*X*X;
}
}
donne sur une O200 Silicon Graphics (processeur R10000),
sous IRIX 6.5.5m et cc 7.2.1,
les résultats suivants en fonction des options d'optimisation :
O200 Silicon Graphics (R10000, IRIX 6.5.5m, cc 7.2.1) :
option '-O2' option '-O3'
X(00) = 0.500000 0.500000
X(10) = 0.384631 0.384631
X(20) = 0.418895 0.418895
X(30) = 0.046399 0.046399
X(40) = 0.320184 0.320192
X(50) = 0.063747 0.059988
X(60) = 0.271115 1.000531
X(70) = 1.328462 1.329692
X(80) = 0.817163 0.021952
Il est facile de calculer simultanément les extrema
de tous les résultats de tous les calculs intermédiaires
lors de chaque opération arithmétique élémentaire.
Le minimum trouve est strictement positif et inférieur à 1,
sans être petit par rapport au plus petit nombre positif représentable.
Le maximum, quant à lui, vaut quelques unités.
Il n'y a donc jamais de calculs élémentaires au cours desquels
seraient combinés deux nombres d'ordres de grandeur très
différents et donc incompatibles avec la représentation
flottante. Il convient de noter au passage que ce dernier problème peut
être lui-aussi la cause de phénomènes "ennuyeux" ; ainsi, à titre
d'exemple, en double précision 64 bits,
additionner 1 à 1e16 ("10 à la puissance 16") est sans effet,
ce qui conduit à l'égalité paradoxale suivante :
16 16
10 + 1 = 10
En ce qui concerne l'influence éventuelle de la syntaxe,
voici une expérience troublante effectuée (avec R = 3.0) en Java
(langage réputé pour son caractère
write once, run everywhere...) avec des variables
déclarées avec le type double :
un même programme calcule sur deux machines différentes
et de cinq façons différentes (mais équivalentes mathématiquement)
l'itération précédente. Voici les résultats obtenus :
O200 Silicon Graphics (processeur R10000, IRIX 6.5.5m, Java) :
(R+1)X-R(XX) (R+1)X-(RX)X ((R+1)-(RX))X RX+(1-(RX))X X+R(X-(XX))
X(0000) = 0.5 0.5 0.5 0.5 0.5
X(0500) = 1.288736212247168 0.007057813075738616 1.2767485100695732 1.246534177059494 0.03910723014701789
X(1000) = 1.3327294162589722 0.916560711983132 1.207710752523091 0.27770146115891703 0.26663342726567785
X(1500) = 1.1448646685382955 0.4481000759915065 0.3102077001456977 0.015374092695375374 0.9841637252962943
X(2000) = 1.0548628914440754 0.896126931497168 0.6851138190159249 0.009229885271816535 0.3860923315999224
X(2500) = 1.292802584458599 0.06063433547953646 1.174118726001978 0.6922411856638806 0.020878761210912034
X(3000) = 1.0497821908090537 0.0219606878364607 1.3287403237319588 0.11354602472378028 0.13270749449424302
X(3500) = 0.8115039383609847 1.3213031319440816 0.6545151597367076 0.5760786099237328 1.324039473116061
X(4000) = 0.04922223042798102 1.3203298564077224 0.09243804931690679 0.9496284087750142 1.316597313359563
X(4500) = 0.4745896653599724 0.32865616721789603 0.018965010461877246 0.25384661313701296 0.18512853535354462
PC (processeur Pentium II, LINUX Mandrake 7.0, Java) :
(R+1)X-R(XX) (R+1)X-(RX)X ((R+1)-(RX))X RX+(1-(RX))X X+R(X-(XX))
X(0000) = 0.5 0.5 0.5 0.5 0.5
X(0500) = 1.2887362122471679 0.00705781307573862 1.2767485100695732 1.2465341770675666 0.03910723014701789
X(1000) = 1.3327294162589722 0.91656071198313205 1.207710752523091 0.6676224369769922 0.26663342726567785
X(1500) = 1.1448646685382955 0.44810007599150647 0.31020770014569771 0.41049165176544455 0.98416372529629426
X(2000) = 1.0548628914440754 0.89612693149716804 0.68511381901592494 1.0026346845706315 0.3860923315999224
X(2500) = 1.3328681064703032 0.06063433547953646 1.1741187260019781 0.0154001182074282 0.02087876121091203
X(3000) = 1.2956769824648844 0.0219606878364607 1.3287403237319588 0.50504896336548377 0.13270749449424302
X(3500) = 0.19193027175727995 0.37986077053509781 0.6545151597367076 0.38299434265835819 1.324039473116061
X(4000) = 1.2491385720940165 0.96017143401896088 0.09243804931690679 0.6565274346305322 1.316597313359563
X(4500) = 0.00644889182443986 1.3185465795235045 0.01896501046187725 0.94966313327336349 0.18512853535354462
Ainsi, il n'est pas surprenant de constater que là-aussi
les cinq formulations donnent des résultats différents.
Par contre, il est étonnant d'observer que trois des
cinq d'entre-elles produisent, sur les deux machines,
des résultats incompatibles, les deux autres donnant des
valeurs identiques (ou presque...).
On notera pour la petite histoire qu'il est essentiel,
dans toutes ces expériences, de préciser
sans ambiguïté les versions du système et du compilateur utilisés,
au cas où ces résultats devraient être reproduits fidèlement.
Il est de plus essentiel de remarquer que d'une part, ce
calcul ne fait appel à aucune méthode numérique (d'intégration par exemple)
et que d'autre part,
ce programme ne peut être faux (ce qui peut être prouvé formellement)...
Moralité : ce programme ne calcule pas l'itération définie ci-dessus
dans le corps des nombres Réels. Oui, mais alors,
qu'étudie-t-il ? Sans que la réponse soit "n'importe quoi",
il faut bien dire que l'itération qui s'exécute effectivement
n'est pas "réellement" connue, car elle dépend d'un
trop grand nombre de paramètres non maitrisés,
voire inconnus...
Augmenter la précision des calculs (l'exemple précédent
utilise la double précision -64 bits-), ne fait
que retarder de quelque peu l'apparition du phénomène
ainsi que le montre cette expérience faite
avec bc
("arbitrary-precision arithmetic language"). Le tableau suivant
donne le numéro d'itération n
à partir duquel la partie entière est fausse,
en fonction du nombre de décimales utilisées pour
faire le calcul (paramètre scale) :
scale = 010 020 030 040 050 060 070 080 090 100
n = 035 070 105 136 169 199 230 265 303 335
Il est évident que le faible gain obtenu ne peut justifier
le coût de cette opération.
Ce qui précède ne doit pas faire croire
qu'un calcul mathématiquement linéaire soit
à l'abri de ces problèmes. Ainsi, examinons
le programme suivant
(sont mises en gras, les lignes réellement essentielles) :
main()
{
double B=4095.1;
double A=B+1;
double x=1;
int n;
printf("initialisation x = %.16f\n",x);
for (n=1 ; n <= 9 ; n++)
{
x = (A*x) - B;
printf("iteration %01d x = %+.16f\n",n,x);
}
}
Les valeurs calculées (après compilation sans optimisation par 'gcc' sur un PC Linux) sont les suivantes :
initialisation x = +1.0000000000000000
iteration 1 x = +1.0000000000004547
iteration 2 x = +1.0000000018630999
iteration 3 x = +1.0000076314440776
iteration 4 x = +1.0312591580864137
iteration 5 x = +129.0406374377594148
iteration 6 x = +524468.2550088063580915
iteration 7 x = +2148270324.2415719032287598
iteration 8 x = +8799530071030.8046875000000000
iteration 9 x = +36043755123945184.0000000000000000
Etant donné l'algorithme et, en particulier, qu'initialement :
x = 1
ainsi qu'il existe la relation suivante :
A-B = 1 (mathématiquement parlant...)
entre les constantes 'A'
(il est a noter qu'avec une partie décimale égale a 0.1, les parties entières posant
problème sont des puissances de 4 ; pour des parties décimales différentes,
la situation est plus complexe...)
et 'B',
la variable 'x' devrait être un invariant et donc rester égale a sa valeur initiale
(1) tout au long des itérations.
Or clairement,
il n'en n'est rien (et ce même apres un très petit nombre d'itérations...).
Au passage, ce programme donne la réponse attendue (1) si l'on remplace
double par float
(ce qui signifie alors tout simplement que, "par hasard",
A-B est égal exactement à 1) ou
encore si une compilation avec optimisation est demandée !
Bien sur, ce phénomène est indépendant du langage de programmation utilisé
(à condition évidemment que les compilateurs et/ou interpréteurs correspondants utilisent les nombres flottants...)
comme cela peut se voir avec les versions en C,
en Fortran 95
ou encore en Python de ce programme sans itérations (pour des raisons de simplicité).
Il conviendra donc de ne pas confondre la
linéarite mathématique et la
linéarite numérique ; cet exemple
est linéaire mathématiquement parlant mais non linéaire au
niveau du calcul numérique (une multiplication par une constante est présente,
or dans la mémoire d'un ordinateur il n'y a que peu de différences entre une
constante et une variable...) !
Au passage, ces constantes d'apparence simple ne sont pas
représentées exactement en machine :
B = 4095.1 = {0x40affe33,33333333}
A = B+1 = 4096.1 = {0x40b00019,9999999a}
A-B = 1.0000000000004547 = {0x3ff00000,00000800}
|
1.0 = {0x3ff00000,00000000}
(les valeurs précédentes ayant ete obtenues avec un PC).
Ce phénomène ne doit pas nous surprendre et est en fait
très commun : ainsi, par exemple, la
fraction 1/3 est une somme finie (un seul terme) d'inverses de puissances de 3
(1/3 s'écrit 0.1 en base 3),
alors que son écriture décimale (0.33333...) est une somme infinie
d'inverses de puissances de 10.
Notons au passage qu'évidemment (et malheureusement...) il n'existe pas de base de numération
grâce à laquelle tous les nombres auraient une représentation finie !
Les conséquences
de tout cela sont nombreuses ; en particulier,
les résultats numériques peuvent ainsi dépendre :
Ces difficultés se rencontreront a priori
avec tous les problèmes dits sensibles aux conditions initiales.
En effet, tout résultat intermédiaire dans un calcul peut être
considéré comme la condition initiale du calcul suivant. Une erreur d'arrondi
dans une valeur constitue donc une imprécision dans les conditions initiales du
calcul qui l'exploite. Mais elles pourront aussi se rencontrer avec des problèmes
linéaire comme cela fut montré précédemment...
La présence de plusieurs précisions différentes à l'intérieur d'un
même programme peut être, elle-aussi,
source de difficultés importantes.
Ainsi le problème dit excess precision problem, connu
des spécialistes du compilateur 'gcc', s'est manifesté
au début de l'année 2004 dans un nouveau programme en cours de développement,
sur pratiquement tous les PCs à processeur de type x86,
sous Linux et avec compilateur 'gcc'.
Il est apparu dans celui-ci qu'un test d'ordre
strict entre deux nombres égaux 'A' et 'B' était vrai et qu'ainsi simultanément
les deux conditions 'A = B' et 'A > B' étaient vérifiées, ce phénomène
n'apparaissant que lors de compilations optimisées (à partir de '-O2').
Les tests effectués et le rôle fondamental
de l'option '-ffloat-store' (inhibant le stockage des nombres flottants
64 bits dans les registres internes 80 bits) qui fait disparaitre le phénomène
ont valide le scénario suivant :
- Soient deux nombres flottants 'A' et 'B' calculés
égaux à l'instant présent et stockés dans les registres
flottants internes 80 bits de l'unité flottante (ou 'FPU')
du processeur (de type x86). Etant tous les deux
représentés par 80 bits significatifs, ils sont "compatibles"
entre-eux ce qui signifie que l'on peut les combiner arithmétiquement
et les comparer sans ambiguité (en particulier, ils
sont présentement égaux : A = B).
- Supposons qu'un manque de ressources flottantes contraigne
le transfert du nombre 'A' en mémoire. A partir de cet instant
'A' n'est plus représenté que par 64 bits significatifs.
Imaginons alors que l'optimiseur ignore ce déplacement
(et c'est bien le cas malheureusement...).
- Supposons ensuite que quelques instructions plus tard
la comparaison de 'A' (stocké sur 64 bits en mémoire)
et de 'B' (toujours stocké sur 80 bits dans un registre) soit
demandée. Le nombre 'A' est donc retransféré dans un
registre 80 bits et donc 80-64=16 bits (nuls très certainement) lui
sont ajoutés. A partir de cet instant-là les deux
nombres 'A' et 'B' ne sont plus "compatibles"
(sauf le cas exceptionnel ou les 16 derniers bits de 'B'
sont nuls) et leur comparaison n'a plus de sens...
- Il est possible d'imaginer de nombreuses autres circonstances
où de telles difficultés apparaissent et par exemple le
cas de deux nombres 'A' et 'B' différents dans une représentation
80 bits et qui deviennent égaux en 64 bits...
Au mois de mars 2004, ce phénomène peut être observé à l'aide du programme suivant :
double f(x)
double x;
{
return(1/x);
}
main()
{
double x1=f(3.0);
volatile double x2;
x2=x1;
if (x2 != x1)
{
printf("DIFFERENT\n");
}
}
Ce programme, lorsqu'il est compilé avec 'gcc -O3 -fno-inline' sur un PC Linux
avec un processeur Intel x86, imprime le message "DIFFERENT" !
Il convient de noter qu'au mois de mars 2018, ce programme fonctionne correctement...
Il convient de noter au passage que la seule solution universelle à ce problème
(c'est-à-dire qui soit à la fois indépendante des architectures matérielles,
des constructeurs, des options de compilation,...) semble être, par
exemple dans le cas des tests, de remplacer ces derniers par des appels
à des fonctions (ceci est trivial à implémenter lors de l'utilisation
du langage K), forçant ainsi
le passage par la pile et donc par une
représentation sur 64 bits. Ainsi le test :
A > B
ou 'A' et 'B' désignent deux nombres flottants 64 bits, pourra s'écrire :
fIFGT(A,B)
la fonction 'fIFGT(...)' étant définie par :
unsigned int fIFGT(x,y)
double x;
double y;
{
return(x > y);
}
et en faisant en sorte qu'elle ne puisse être développée (inlined)
par le compilateur (option '-fno-inline' de 'gcc')...
Ainsi, augmenter la précision et/ou utiliser simultanément plusieurs
précisions différentes peut entrainer des difficultés et des complications imprevues...
Le passage par des fonctions pour exécuter les instructions élémentaires
(addition, soustraction, multiplication, division, tests,...)
d'un programme, même s'il est parfois pénalisant au niveau des
performances, possède un autre avantage :
il permet d'imposer l'ordre d'exécution de celles-ci,
alors qu'ainsi que cela fut montre précédemment, celui-ci peut influer
de façon plus ou moins importante, voire dramatique,
sur les résultats obtenus.
En effet, en toute généralité :
F.G # G.F
'F' et 'G' désignant deux fonctions arbitraires ; les compilateurs
n'ont donc absolument pas le droit de remplacer 'F(G(...))' par 'G(F(...))'.
Ainsi, par exemple,
ces deux images  et
et  ,
calculées à l'aide d'un processus non itératif
sur la même machine (un PC sous Linux), avec et sans imposer l'ordre respectivement,
semblent identiques,
alors qu'elles sont en réalité légèrement différentes.
Au passage, l'utilisation de fonctions présente un autre avantage :
celui de permettre l'extension de l'arithmétique.
,
calculées à l'aide d'un processus non itératif
sur la même machine (un PC sous Linux), avec et sans imposer l'ordre respectivement,
semblent identiques,
alors qu'elles sont en réalité légèrement différentes.
Au passage, l'utilisation de fonctions présente un autre avantage :
celui de permettre l'extension de l'arithmétique.
Ainsi, ces problèmes peuvent se manifester même en dehors des systèmes
itératifs. Dans ces derniers les erreurs d'arrondis se trouvent amplifiées
numériquement lors des calculs successifs, alors que dans les cas illustrés par
l'exemple précédent, l'amplification peut être d'une autre nature.
Ici, elle peut être qualifiée de "visuelle" et s'analyse de la façon
suivante : imaginons deux points P1(x1,y1,z1) et P2(x2,y2,z2) mathématiquement identiques
(x1=x2, y1=y2 et z1=z2) et ne différant que par leur couleur (rouge pour P1 et vert
pour P2). Supposons l'axe 'OZ' orthogonal au plan de l'image et orienté vers l'observateur.
Puis imaginons que la compilation
du programme ait lieu sur deux machines identiques, à la version de leur compilateur près.
Nous pourrons obtenir (et c'est le phénomène rencontré dans l'exemple précédent !)
{x1=x2, y1=y2 et z1>z2} sur la première (d'ou un point rouge -P1 est devant P2-)
et {x2=x1, y2=y1 et z2>z1} sur la seconde (d'ou un point vert -P2 est devant P1-)...
Enfin, utiliser l'arithmétique dite
d'intervalle, semble
aussi voué à l'échec sur les problèmes sensibles aux conditions initiales
(comme l'est l'exemple précédent). En effet, un intervalle
[x-epsilon,x+epsilon] encadrant une valeur exacte ne peut,
en toute généralité, qu'"exploser" au cours
des calculs suivants,
puisque 'x-epsilon' et 'x+epsilon' peuvent être considérées
comme deux conditions initiales très voisines l'une de l'autre...
Le problème des N-corps donne
un exemple concret de ces difficultés.
Alors, ne pourrait-on pas se passer des Nombres Réels pour faire de la physique mathématique ?
Pour en terminer avec cette "affaire" résumons visuellement, par l'exemple,
quelques unes des conséquences des erreurs d'arrondi :
-
 L'irréversibilité numérique du billard bidimensionnel -1376 particules-. Un système réversible peut perdre cette proprieté s'il est
sensible aux erreurs d'arrondi. Dans cet exemple,
au "milieu temporel" du calcul, tous les vecteurs vitesses
sont "inversés". L'état final obtenu est malheureusement
très différent de l'état initial.
L'irréversibilité numérique du billard bidimensionnel -1376 particules-. Un système réversible peut perdre cette proprieté s'il est
sensible aux erreurs d'arrondi. Dans cet exemple,
au "milieu temporel" du calcul, tous les vecteurs vitesses
sont "inversés". L'état final obtenu est malheureusement
très différent de l'état initial.
-
 Visualisation bidimensionnelle des erreurs d'arrondi dans le calcul de la dynamique de Verhulst
[Plus d'informations].
De la façon d'écrire un programme (et en particulier de la façon
de parenthéser) peuvent dépendre les résultats.
Visualisation bidimensionnelle des erreurs d'arrondi dans le calcul de la dynamique de Verhulst
[Plus d'informations].
De la façon d'écrire un programme (et en particulier de la façon
de parenthéser) peuvent dépendre les résultats.
-
 Rotation autour de l'axe X de l'attracteur de Lorenz
(uniquement afin de mieux comprendre les images suivantes).
Rotation autour de l'axe X de l'attracteur de Lorenz
(uniquement afin de mieux comprendre les images suivantes).
-
 L'attracteur de Lorenz -sensibilité aux conditions initiales (la Rouge, la Verte et la Bleue)-.
L'attracteur de Lorenz -sensibilité aux conditions initiales (la Rouge, la Verte et la Bleue)-.
-
 L'attracteur de Lorenz -sensibilité à la méthode d'intégration utilisée (Rouge=Euler, Vert=Runge-Kutta/second ordre, Bleu=Runge-Kutta/quatrième ordre)-.
L'attracteur de Lorenz -sensibilité à la méthode d'intégration utilisée (Rouge=Euler, Vert=Runge-Kutta/second ordre, Bleu=Runge-Kutta/quatrième ordre)-.
-
 Calcul de l'attracteur de Lorenz sur trois ordinateurs différents (le Rouge, le Vert et le Bleu : sensibilité aux erreurs d'arrondi). Ainsi un système sensible aux conditions initiales (comme l'est
l'attracteur de Lorenz) est sensible aux erreurs d'arrondi (et réciproquement ?).
Calcul de l'attracteur de Lorenz sur trois ordinateurs différents (le Rouge, le Vert et le Bleu : sensibilité aux erreurs d'arrondi). Ainsi un système sensible aux conditions initiales (comme l'est
l'attracteur de Lorenz) est sensible aux erreurs d'arrondi (et réciproquement ?).
-
 Rotation autour de l'axe X de l'attracteur de Lorenz (1000 itérations), calculée sur deux ordinateurs différents. Ce mouvement de rotation calculé conjointement par deux ordinateurs
différents semble correct. En effet, le calcul ne portant
que sur 1000 itérations, l'anomalie finale n'est pas encore suffisamment
importante pour être visible.
Rotation autour de l'axe X de l'attracteur de Lorenz (1000 itérations), calculée sur deux ordinateurs différents. Ce mouvement de rotation calculé conjointement par deux ordinateurs
différents semble correct. En effet, le calcul ne portant
que sur 1000 itérations, l'anomalie finale n'est pas encore suffisamment
importante pour être visible.
-
 Rotation autour de l'axe X de l'attracteur de Lorenz (5000 itérations), calculée sur deux ordinateurs différents. Cette fois-ci, le mouvement de rotation semble incorrect
(bien observer les saccades entre certains couples d'images).
En effet, le calcul porte ici sur 5000 itérations ce qui
laisse le temps à l'anomalie de s'amplifier suffisamment pour être visible
à la fin de ce processus.
Cette expérience, combinée avec la précédente,
montre la difficulté de faire du calcul parallèle portant sur des
modèles sensibles aux erreurs d'arrondi, à l'aide d'un
ensemble de machines hétérogènes (aussi bien au niveau matériel
qu'au niveau logiciel -une simple différence de version du compilateur utilisé
peut suffire !-).
Rotation autour de l'axe X de l'attracteur de Lorenz (5000 itérations), calculée sur deux ordinateurs différents. Cette fois-ci, le mouvement de rotation semble incorrect
(bien observer les saccades entre certains couples d'images).
En effet, le calcul porte ici sur 5000 itérations ce qui
laisse le temps à l'anomalie de s'amplifier suffisamment pour être visible
à la fin de ce processus.
Cette expérience, combinée avec la précédente,
montre la difficulté de faire du calcul parallèle portant sur des
modèles sensibles aux erreurs d'arrondi, à l'aide d'un
ensemble de machines hétérogènes (aussi bien au niveau matériel
qu'au niveau logiciel -une simple différence de version du compilateur utilisé
peut suffire !-).
-
 Intégration du problème des N-corps (N=4 : une étoile, une planète lourde et une planète légère avec un satellite) calculé avec 2 options d'optimisation différentes (sensibilité aux erreurs d'arrondi).
Intégration du problème des N-corps (N=4 : une étoile, une planète lourde et une planète légère avec un satellite) calculé avec 2 options d'optimisation différentes (sensibilité aux erreurs d'arrondi).
Heureusement, tous les problèmes traités sur ordinateur ne sont pas aussi
sensibles aux erreurs d'arrondi (bien qu'elles soient évidemment toujours présentes).
Mais les exemples précédents, par leur "brutalité", montrent l'existence
de ce phénomène en rappelant que dans certaines circonstances les résultats obtenus
peuvent être, non pas approchés, mais "tout simplement" faux...
4.4-La Visualisation :
En ce qui concerne la visualisation,
contrairement à la synthèse d'image
spectaculaire telle celle-ci  , il
s'agit, dans le contexte de l'Expérimentation Virtuelle, de montrer bien souvent des objets
sans image, soit qu'ils n'existent pas dans la
nature (tel cet ensemble de Julia dans les quaternions
, il
s'agit, dans le contexte de l'Expérimentation Virtuelle, de montrer bien souvent des objets
sans image, soit qu'ils n'existent pas dans la
nature (tel cet ensemble de Julia dans les quaternions  ),
soit que, bien qu'étant
naturels, il soit impossible, voire interdit, de
les représenter (comme l'atome d'hydrogène
),
soit que, bien qu'étant
naturels, il soit impossible, voire interdit, de
les représenter (comme l'atome d'hydrogène  ) ou encore
tout simplement parce qu'ils n'ont pas
d'équivalents visuels (une pression ou une
température par exemple...). S'il est clair
que montrer un objet à quatre dimensions
est chose difficile (tel
) ou encore
tout simplement parce qu'ils n'ont pas
d'équivalents visuels (une pression ou une
température par exemple...). S'il est clair
que montrer un objet à quatre dimensions
est chose difficile (tel  ), il est
malheureusement moins évident que toute
tentative de représentation, dans ce
domaine, est délicate. La difficulte vient
bien entendu des espaces, en général non
naturels, dans lesquels résident ces objets,
mais surtout de la non unicité des images
que l'on peut en donner : même dans les cas
les plus simples, des ambiguités et des
contradictions peuvent surgir. En toute généralite,
il n'y a pas unicité de la représentation.
), il est
malheureusement moins évident que toute
tentative de représentation, dans ce
domaine, est délicate. La difficulte vient
bien entendu des espaces, en général non
naturels, dans lesquels résident ces objets,
mais surtout de la non unicité des images
que l'on peut en donner : même dans les cas
les plus simples, des ambiguités et des
contradictions peuvent surgir. En toute généralite,
il n'y a pas unicité de la représentation.
Ainsi, la visualisation d'un tableau de nombres
pourrait être considérée, naïvement, comme une opération
élémentaire et bien maitrisée depuis de nombreuses
décennies. En effet, la géographie ou la météorologie font
appel à des couleurs pour représenter des altitudes, des
températures ou encore des pressions. Malheureusement,
cette simplicité n'est qu'apparente : ces quatre images  nous
montrent le même ensemble bidimensionnel (un "tableau") de nombres, la
seule différence se situant dans le code des couleurs
utilisées. En effet, pour obtenir ce type de représentation, il
suffit d'associer aux nombres (ou plus généralement à des
plages de valeurs numériques) des couleurs (en appelant aussi
couleur, par abus de langage, le noir, les gris et le blanc) ;
par exemple, il sera décide arbitrairement de représenter par
du rouge les points associés à des valeurs numériques
comprises entre 1.37 et 3.62. De cet arbitraire naissent les
difficultés ici presentées. De toute évidence, dans cet exemple, la perception
varie fortement d'une image à l'autre, les conclusions
possibles sur l'unique tableau de nombres sous-jacent
pouvant même être en contradiction les unes avec les autres !
Ces quatre représentations peuvent être qualifiées d'orthogonales...
Une sémiologie de la Visualisation Scientifique reste à créer ;
elle serait un lieu de rencontre privilégié entre les artistes et
les scientifiques.
nous
montrent le même ensemble bidimensionnel (un "tableau") de nombres, la
seule différence se situant dans le code des couleurs
utilisées. En effet, pour obtenir ce type de représentation, il
suffit d'associer aux nombres (ou plus généralement à des
plages de valeurs numériques) des couleurs (en appelant aussi
couleur, par abus de langage, le noir, les gris et le blanc) ;
par exemple, il sera décide arbitrairement de représenter par
du rouge les points associés à des valeurs numériques
comprises entre 1.37 et 3.62. De cet arbitraire naissent les
difficultés ici presentées. De toute évidence, dans cet exemple, la perception
varie fortement d'une image à l'autre, les conclusions
possibles sur l'unique tableau de nombres sous-jacent
pouvant même être en contradiction les unes avec les autres !
Ces quatre représentations peuvent être qualifiées d'orthogonales...
Une sémiologie de la Visualisation Scientifique reste à créer ;
elle serait un lieu de rencontre privilégié entre les artistes et
les scientifiques.
De plus, il est souvent tellement facile de
calculer de telles images, que le risque peut
être grand de confondre esthétisme et valeur
scientifique : une belle représentation n'est
point nécessairement bonne (que vaut, par exemple,
cette image  ),
alors que, bien souvent, ce critère
d'harmonie est utilisé pour juger une
théorie scientifique (c'était, par exemple, la démarche
suivie par Paul Dirac). Malgré cela, il ne faudrait pas
négliger l'apport de l'Art à la Science. En
effet, il est des codes culturels définis au
cours des siècles passés ; ceux-ci doivent
être respectés ici sous peine, dans le cas
contraire, de produire des visualisations qui
soient en contradiction avec nos mécanismes
perceptifs. A titre d'exemple, une couleur
dite froide (respectivement chaude) est en
général associée à des valeurs numériques
faibles (respectivement élevées) et cette
convention quasi universelle doit ici
s'appliquer.
),
alors que, bien souvent, ce critère
d'harmonie est utilisé pour juger une
théorie scientifique (c'était, par exemple, la démarche
suivie par Paul Dirac). Malgré cela, il ne faudrait pas
négliger l'apport de l'Art à la Science. En
effet, il est des codes culturels définis au
cours des siècles passés ; ceux-ci doivent
être respectés ici sous peine, dans le cas
contraire, de produire des visualisations qui
soient en contradiction avec nos mécanismes
perceptifs. A titre d'exemple, une couleur
dite froide (respectivement chaude) est en
général associée à des valeurs numériques
faibles (respectivement élevées) et cette
convention quasi universelle doit ici
s'appliquer.
Enfin, il ne faut pas oublier que, par définition,
ces images sont faites pour être regardées. Or le système visuel n'est lui-même
pas exempt de défauts. Des illusions d'optique peuvent donc survenir et par exemple :
5-CONCLUSION :
Une fois avertis de ces dangers, les
scientifiques et les ingénieurs ont à leur
disposition un nouvel instrument dont les
implications épistémologiques auront au
moins l'importance de la lunette de
Galilée en son temps. Tout ceci débouche
sur le concept d'Expérimentation Virtuelle.
Cette dernière, complémentaire de
l'Expérimentation Réelle (le qualificatif réel étant ici utilisé, rappelons-le, dans son
sens le plus intuitif et loin de tout débat sur la notion de Réalité), consiste donc,
tant dans les domaines scientifique
qu'industriel, à faire des expériences non
point sur un système réel (cela étant sricto sensu de plus en plus
difficile ; par exemple, quel physicien a dejà touché une particule élémentaire ?), mais sur son
modèle mathématique (voir l'annexe 2) et à
interagir avec ce dernier par l'intermédiaire
d'images de synthèse. Alors, en restant -ou pas...-
dans le cadre de légalité des lois de la
nature, tout nous est permis, et par exemple
de créer les univers utiles à nos recherches
(comme  ou encore
ou encore  ).
).
Bien évidemment de nombreuses
questions surgissent de cette approche.
D'une part, la science et, en particulier, les
mathématiques ont-elles droit à ces images ?
Et d'ailleurs sont-elles utiles ? Le
scientifique ne peut-il se contenter de la
seule pensée verbale et bannir alors toute
aide visuelle ? Un élément de réponse à cette
interrogation fut donné par Albert Einstein
dans une lettre qu'il écrivit à Jacques
Hadamard : "les mots et le langage, écrits ou
parlés, ne semblent pas jouer le moindre
rôle dans le mécanisme de ma pensée. Les
entités psychiques qui servent d'éléments à
la pensée sont certains signes ou des images
plus ou moins claires qui peuvent à volonté
être reproduits et combinés". Il convient de
se souvenir que pendant plusieurs
décennies, un large mouvement
d'abstraction (dans l'œuvre de Nicolas Bourbaki en particulier) s'est imposé mais que,
l'apparition de nouvelles techniques aidant
(ordinateur et synthèse d'image en
particulier), nous assistons aujourd'hui à un
retour en force de la pensée visuelle. Bien
évidemment tout extrémisme est dangereux,
ici comme ailleurs ; il ne faudrait pas qu'un
mouvement inverse se déclenche et que le
je pense donc je suis
se transforme en un
je calcule et je visualise donc je suis...
A titre d'exemple, rappelons que la géométrie
fractale a très certainement pris l'essor
qu'elle connait actuellement grâce à l'image,
mais que, malgré cela, il n'est jamais de
certitudes visuelles et que les conjectures qui
peuvent être formulées à partir d'une
représentation doivent se voir confirmées ou
infirmées par un theorème demontré "à l'ancienne" (voir, par exemple,
l'histoire de la conjecture -demontrée fausse par la suite- de la non connexité de l'ensemble de Mandelbrot-) !
L'image doit donc être vue ici simplement comme un
levier intellectuel stimulant et entrainant plus
loin l'imagination du chercheur, rendant
ainsi toute sa noblesse au sens de la vision.
D'autre part, ces univers crées dans nos
ordinateurs ont-ils le statut ontologique de
nouvelles réalités ?
Ces "univers-jouets" avec leurs lois
calquées sur celles de la nature, ou bien avec
d'autres sur lesquelles il nous faut
expérimenter, ne sont-ils pas aussi réels que
celui que nous n'appréhendons finalement
que par les modèles neuronaux crées par
nos sens au cours des âges ? Enfin, ces
images de science, si elles créent bien
souvent la surprise chez ceux qui en ont un
besoin immédiat et professionnel,
interpellent fréquemment la sensibilité du
profane et de l'artiste, signe certain d'un
contenu beaucoup plus riche que les
apparences ne le laisseraient parfois
supposer. Ne sont-elles point alors à
entendre comme un lieu de convergence
entre l'Art et la Science, ou tout reste encore
à voir et à découvrir ?
ANNEXE 1 :
A titre d'exemple de
modèle, examinons brièvement le problème
dit des N corps. Etant donné N objets
massiques, mais supposes ponctuels, il
s'agit d'étudier leurs interactions
gravitationnelles à partir de certaines
conditions initiales définies à l'instant 0 par
l'ensemble des coordonnées et des vitesses.
Cette étude doit donc nous fournir pour tout
instant futur les positions et les vitesses de
chacun de ces corps. Les équations du
problème, dans le cadre de la mécanique
newtonienne, peuvent être écrites facilement
par un élève de terminale S ; mais est-il aisé
d'aller ensuite plus avant ? Grâce à
Johannes Kepler (Astronomia Nova, 1609)
et à sir Isaac Newton (Philosophiae
Naturalis Principia Mathematica, 1687) nous
savons que pour N égal à 2, l'un des deux
corps décrit une ellipse dont l'un des foyers
est le second d'entre-eux. Mais pour les
valeurs de N supérieures à 2, que se
passe-t-il ? Pour la réponse à cette question,
il à fallu attendre deux cents ans avec les
travaux de Henri Poincare (Les méthodes
nouvelles de la mécanique céleste,
1892-1899) ; ce dernier a montré que, bien
que les équations soient "simples" comme
nous l'avons noté précedemment, ce
problème n'avait pas de solution. Ainsi,
nous sommes incapables d'écrire des
formules exactes qui nous donneraient les
informations recherchées (comme, par exemple, dans le cas  ).
).
ANNEXE 2 :
Pour mettre en œuvre le
concept d'Expérimentation Virtuelle, il nous
faut construire un système informatique
approprié. Il peut aujourd'hui reposer sur le
concept de meta-ordinateur,
assemblage logique (mais non physique) de machines de
calcul, de stockage, de visualisation et
d'interaction (pouvant utiliser, en
particulier, les techniques dites de Réalité
Virtuelle), mais aussi d'appareils de mesure
(par exemple, le télescope spatial Hubble).
Ces différentes composantes n'ont pas
besoin d'être physiquement proches l'une
de l'autre ; bien au contraire, elles peuvent
être réparties sur la planète entière,
constituant ainsi des machines, elles-aussi
virtuelles, d'une puissance phénoménale.
Cette ubiquité électronique est aujourd'hui
rendue possible par les réseaux
informatiques, dont le plus connu et le plus
universel est actuellement Internet ; les
lecteurs sont invités
à se connecter au serveur
A VIRTUAL SPACE-TIME TRAVEL MACHINE
qui présente de multiples applications
opérationnelles de l'Expérimentation
Virtuelle, ainsi que de nombreuses
explications complémentaires à cet article.
Son nom, A Virtual Space-Time Travel Machine
(une machine virtuelle à voyager dans l'espace-temps),
a été choisi afin de résumer en une seule
expression les possibilités de certains outils
de la Science contemporaine...
Copyright © Jean-François COLONNA, 2002-2025.
Copyright © France Telecom R&D and CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2002-2025.

 , qui fut le premier
dont l'auteur a pu disposer à titre professionnel en 1972, disposait, à l'intérieur de
ses armoires de trois mètres cubes, d'une "phénoménale" mémoire centrale de 32 kilo-octets
et de trois disques durs de chacun un demi méga-octet !
Aujourd'hui (au mois de novembre 2002), les ordinateurs portables les plus performants
disposent d'horloges de deux giga-hertz,
intégrent des mémoires centrales d'un giga-octet (Go) et des disques de plusieurs dizaines de Go.
Il semble que cette course aux performances soit faite pour se poursuivre dans les années à venir.
Evidemment, la technonologie actuelle possède des limites, mais celles-ci
sont relativement éloignées (et d'ailleurs l'histoire montre qu'elles sont fréquemment repoussées...).
D'autre part, de nouvelles façons d'utiliser les ordinateurs permettent d'atteindre
des capacités de traitement et de stockage absolument phénoménales. C'est en particulier
le cas avec la notion de méta-ordinateur
qui permet de concevoir des systèmes virtuels répartis (éventuellement sur la Terre entière)
n'utilisant que des systèmes standards et bon marché.
Et au-delà, les recherches les plus avancées nous annoncent
l'ordinateur quantique, mais
pourra-t-il être construit au-delà de quelques prototypes de laboratoire capables actuellement
de factoriser de petits nombres à deux chiffres (il convient de rappeler que l'un des attraits
de ces machines, reposant sur le principe de superposition linéaire cher à la Mécanique Quantique,
est d'offrir, par rapport aux machines "classiques", la possibilité de factoriser
beaucoup plus rapidement les nombres entiers -algorithme de Schorr-, avec des conséquences
évidentes en ce qui concerne de nombreuses méthodes de chiffrement...) ?
, qui fut le premier
dont l'auteur a pu disposer à titre professionnel en 1972, disposait, à l'intérieur de
ses armoires de trois mètres cubes, d'une "phénoménale" mémoire centrale de 32 kilo-octets
et de trois disques durs de chacun un demi méga-octet !
Aujourd'hui (au mois de novembre 2002), les ordinateurs portables les plus performants
disposent d'horloges de deux giga-hertz,
intégrent des mémoires centrales d'un giga-octet (Go) et des disques de plusieurs dizaines de Go.
Il semble que cette course aux performances soit faite pour se poursuivre dans les années à venir.
Evidemment, la technonologie actuelle possède des limites, mais celles-ci
sont relativement éloignées (et d'ailleurs l'histoire montre qu'elles sont fréquemment repoussées...).
D'autre part, de nouvelles façons d'utiliser les ordinateurs permettent d'atteindre
des capacités de traitement et de stockage absolument phénoménales. C'est en particulier
le cas avec la notion de méta-ordinateur
qui permet de concevoir des systèmes virtuels répartis (éventuellement sur la Terre entière)
n'utilisant que des systèmes standards et bon marché.
Et au-delà, les recherches les plus avancées nous annoncent
l'ordinateur quantique, mais
pourra-t-il être construit au-delà de quelques prototypes de laboratoire capables actuellement
de factoriser de petits nombres à deux chiffres (il convient de rappeler que l'un des attraits
de ces machines, reposant sur le principe de superposition linéaire cher à la Mécanique Quantique,
est d'offrir, par rapport aux machines "classiques", la possibilité de factoriser
beaucoup plus rapidement les nombres entiers -algorithme de Schorr-, avec des conséquences
évidentes en ce qui concerne de nombreuses méthodes de chiffrement...) ?
 montre instantanément et sans effort de
réflexion, que les trajectoires de ce problème à quatre corps utilisant
les conditions initiales suivantes (données en unités MKSA et visualisées en bas et à gauche de cette matrice de 16 images) :
montre instantanément et sans effort de
réflexion, que les trajectoires de ce problème à quatre corps utilisant
les conditions initiales suivantes (données en unités MKSA et visualisées en bas et à gauche de cette matrice de 16 images) :
 Représentation tridimensionnelle d'une variété quadridimensionnelle de Calabi-Yau
Représentation tridimensionnelle d'une variété quadridimensionnelle de Calabi-Yau Structure en quarks et gluons du nucléon
Structure en quarks et gluons du nucléon Visualisation tridimensionnelle de la superposition linéaire de 6 états propres de l'atome d'Hydrogène (calcul tridimensionnel)
Visualisation tridimensionnelle de la superposition linéaire de 6 états propres de l'atome d'Hydrogène (calcul tridimensionnel) Les deux premières itérations de la construction de la courbe de von Koch
Les deux premières itérations de la construction de la courbe de von Koch Le long de la frontière de l'ensemble de Mandelbrot
Le long de la frontière de l'ensemble de Mandelbrot L'ensemble de Julia dans le corps des quaternions calculé pour A=(0,1,0,0) -ou 'la danseuse d'Yr'- -section tridimensionnelle-
L'ensemble de Julia dans le corps des quaternions calculé pour A=(0,1,0,0) -ou 'la danseuse d'Yr'- -section tridimensionnelle- Ensembles de Julia dans le corps des quaternions lors d'une promenade autour de l'ensemble de Mandelbrot -coupes tridimensionnelles-
Ensembles de Julia dans le corps des quaternions lors d'une promenade autour de l'ensemble de Mandelbrot -coupes tridimensionnelles- Rotation de 2.pi autour des axes Y et Z d'un ensemble de Julia dans le corps des quaternions -section tridimensionnelle-
Rotation de 2.pi autour des axes Y et Z d'un ensemble de Julia dans le corps des quaternions -section tridimensionnelle- Le processus itératif de génération de champs fractals bidimensionnels (16 itérations)
Le processus itératif de génération de champs fractals bidimensionnels (16 itérations) Le processus itératif de génération de montagnes fractales (16 itérations)
Le processus itératif de génération de montagnes fractales (16 itérations) Montagnes au lever du Soleil
Montagnes au lever du Soleil Montagnes et dynamique de nuages légers -cette séquence étant périodique-
Montagnes et dynamique de nuages légers -cette séquence étant périodique- L'érosion de la Tour de Babel
L'érosion de la Tour de Babel Tremblement de terre sur des montagnes multi-fractales
Tremblement de terre sur des montagnes multi-fractales Monument Valley au lever du Soleil
Monument Valley au lever du Soleil Monument Valley dansante
Monument Valley dansante L'anomalie de Botticelli sur la Lune
L'anomalie de Botticelli sur la Lune Structure fractale tridimensionnelle
Structure fractale tridimensionnelle Marche aléatoire isotrope de 4 particules sur un réseau carré bidimensionnel avec visualisation de leur centre de gravité -particule blanche-
Marche aléatoire isotrope de 4 particules sur un réseau carré bidimensionnel avec visualisation de leur centre de gravité -particule blanche- Marche aléatoire isotrope de 256 particules sur un réseau carré bidimensionnel avec visualisation de leur centre de gravité -particule blanche-
Marche aléatoire isotrope de 256 particules sur un réseau carré bidimensionnel avec visualisation de leur centre de gravité -particule blanche- Billard bidimensionnel rectangulaire avec 4 particules aléatoires en collision et visualisation de leur centre de gravité -particule blanche-
Billard bidimensionnel rectangulaire avec 4 particules aléatoires en collision et visualisation de leur centre de gravité -particule blanche- Billard bidimensionnel rectangulaire avec 256 particules aléatoires en collision et visualisation de leur centre de gravité -particule blanche-
Billard bidimensionnel rectangulaire avec 256 particules aléatoires en collision et visualisation de leur centre de gravité -particule blanche- Billard bidimensionnel de Sierpinski avec 4 particules aléatoires en collision et visualisation de leur centre de gravité -particule blanche-
Billard bidimensionnel de Sierpinski avec 4 particules aléatoires en collision et visualisation de leur centre de gravité -particule blanche- Billard bidimensionnel de Sierpinski avec 256 particules aléatoires en collision et visualisation de leur centre de gravité -particule blanche-
Billard bidimensionnel de Sierpinski avec 256 particules aléatoires en collision et visualisation de leur centre de gravité -particule blanche- Diffusion entre deux boîtes (conditions initiales : la boîte de gauche est vide alors que la boîte de droite contient 256 particules), avec collisions et une géométrie variable
Diffusion entre deux boîtes (conditions initiales : la boîte de gauche est vide alors que la boîte de droite contient 256 particules), avec collisions et une géométrie variable Front fractal de diffusion dans un milieu bidimensionnel obtenu grâce à des particules identiques en interaction
Front fractal de diffusion dans un milieu bidimensionnel obtenu grâce à des particules identiques en interaction L'effet domino bidimensionnel
L'effet domino bidimensionnel Mouvement brownien de quelques particules lourdes dans un gaz de particules légères et rapides
Mouvement brownien de quelques particules lourdes dans un gaz de particules légères et rapides Mouvement brownien de quelques particules lourdes et lumineuses dans un gaz de particules légères et rapides, avec un rapport croissant des rapports de masse (lourdes/légères=1,10,100,1000)
Mouvement brownien de quelques particules lourdes et lumineuses dans un gaz de particules légères et rapides, avec un rapport croissant des rapports de masse (lourdes/légères=1,10,100,1000) Particules en collision sans perte d'énergie dans un espace bidimensionnel avec visualisation de l'histogramme des modules des vitesses
Particules en collision sans perte d'énergie dans un espace bidimensionnel avec visualisation de l'histogramme des modules des vitesses Particules en collision sans perte d'énergie dans un espace tridimensionnel avec visualisation de l'histogramme des modules des vitesses
Particules en collision sans perte d'énergie dans un espace tridimensionnel avec visualisation de l'histogramme des modules des vitesses Détente d'un gaz dans une boîte circulaire bidimensionnelle avec visualisation de l'histogramme des modules des vitesses
Détente d'un gaz dans une boîte circulaire bidimensionnelle avec visualisation de l'histogramme des modules des vitesses Billard bidimensionnel de Sierpinski avec 326 particules isotropes soumises à un fort champ de gravitation vertical
Billard bidimensionnel de Sierpinski avec 326 particules isotropes soumises à un fort champ de gravitation vertical Un piston bidimensionnel parfait avec les conditions initiales suivantes : piston immobîle, particules chaudes à gauche et froides à droite, le tout dans une boîte bidimensionnelle soumise à un champ de gravitation vertical
Un piston bidimensionnel parfait avec les conditions initiales suivantes : piston immobîle, particules chaudes à gauche et froides à droite, le tout dans une boîte bidimensionnelle soumise à un champ de gravitation vertical Un fluide bidimensionnel périodique avec des vitesses strictement identiques initialement et un obstacle central très légèrement décale verticalement, avec visualisation de l'histogramme des modules des vitesses
Un fluide bidimensionnel périodique avec des vitesses strictement identiques initialement et un obstacle central très légèrement décale verticalement, avec visualisation de l'histogramme des modules des vitesses Agrégats fractals bidimensionnels obtenus par collage de 100% des particules lors de leurs collisions, dans un champ de gravitation central attractif
Agrégats fractals bidimensionnels obtenus par collage de 100% des particules lors de leurs collisions, dans un champ de gravitation central attractif Agrégats fractals bidimensionnels obtenus par collage de 50% des particules lors de leurs collisions, dans un champ de gravitation central attractif
Agrégats fractals bidimensionnels obtenus par collage de 50% des particules lors de leurs collisions, dans un champ de gravitation central attractif Agrégats fractals bidimensionnels obtenus par collage de 100% des particules lors de leurs collisions, dans un champ de gravitation vertical
Agrégats fractals bidimensionnels obtenus par collage de 100% des particules lors de leurs collisions, dans un champ de gravitation vertical Agrégats fractals bidimensionnels obtenus par collage de 50% des particules lors de leurs collisions, dans un champ de gravitation vertical
Agrégats fractals bidimensionnels obtenus par collage de 50% des particules lors de leurs collisions, dans un champ de gravitation vertical Agrégat fractal tridimensionnel obtenu par collage de 100% des particules lors de leurs collisions, dans un champ de gravitation central
Agrégat fractal tridimensionnel obtenu par collage de 100% des particules lors de leurs collisions, dans un champ de gravitation central Agrégat fractal tridimensionnel obtenu par collage de 50% des particules lors de leurs collisions, dans un champ de gravitation central
Agrégat fractal tridimensionnel obtenu par collage de 50% des particules lors de leurs collisions, dans un champ de gravitation central Agrégats fractals tridimensionnels obtenus par collage de 100% des particules lors de leurs collisions, dans un champ de gravitation vertical
Agrégats fractals tridimensionnels obtenus par collage de 100% des particules lors de leurs collisions, dans un champ de gravitation vertical Agrégats fractals tridimensionnels obtenus par collage de 50% des particules lors de leurs collisions, dans un champ de gravitation vertical
Agrégats fractals tridimensionnels obtenus par collage de 50% des particules lors de leurs collisions, dans un champ de gravitation vertical La marche aléatoire des photons produits au cœur du Soleil
La marche aléatoire des photons produits au cœur du Soleil Diffusion de particules à l'intérieur du modèle de l'acinus pulmonaire humain dû à Hiroko Kitaoka
Diffusion de particules à l'intérieur du modèle de l'acinus pulmonaire humain dû à Hiroko Kitaoka Diffusion de particules à l'intérieur du modèle de l'acinus pulmonaire humain dû à Hiroko Kitaoka avec perméabilité de la membrane
Diffusion de particules à l'intérieur du modèle de l'acinus pulmonaire humain dû à Hiroko Kitaoka avec perméabilité de la membrane Diffusion de particules à l'intérieur du modèle de l'acinus pulmonaire humain dû à Hiroko Kitaoka avec perméabilité de la membrane
Diffusion de particules à l'intérieur du modèle de l'acinus pulmonaire humain dû à Hiroko Kitaoka avec perméabilité de la membrane Visualisation de l'inclinaison de deux trajectoires elliptiques
Visualisation de l'inclinaison de deux trajectoires elliptiques Intégration du problème des N-corps (N=10) montrant le véritable système solaire avec une rotation simultanée de 2.pi
Intégration du problème des N-corps (N=10) montrant le véritable système solaire avec une rotation simultanée de 2.pi Intégration du problème des N-corps (N=10) montrant le véritable système solaire avec une rotation simultanée de 2.pi, notre Terre étant choisie comme origine des coordonnées
Intégration du problème des N-corps (N=10) montrant le véritable système solaire avec une rotation simultanée de 2.pi, notre Terre étant choisie comme origine des coordonnées De Pluton au Soleil (échelles non linéaires)
De Pluton au Soleil (échelles non linéaires) Simulation de 'de Pluton au Soleil' avec de purs mouvements circulaires uniformes (échelles linéaires)
Simulation de 'de Pluton au Soleil' avec de purs mouvements circulaires uniformes (échelles linéaires) De Pluton au Soleil -extrapolation 1- (échelles non linéaires)
De Pluton au Soleil -extrapolation 1- (échelles non linéaires) et
et  ,
calculées à l'aide d'un processus non itératif
sur la même machine (un PC sous Linux), avec et sans imposer l'ordre respectivement,
semblent identiques,
alors qu'elles sont en réalité légèrement différentes.
Au passage, l'utilisation de fonctions présente un autre avantage :
celui de permettre l'extension de l'arithmétique.
,
calculées à l'aide d'un processus non itératif
sur la même machine (un PC sous Linux), avec et sans imposer l'ordre respectivement,
semblent identiques,
alors qu'elles sont en réalité légèrement différentes.
Au passage, l'utilisation de fonctions présente un autre avantage :
celui de permettre l'extension de l'arithmétique.
 L'irréversibilité numérique du billard bidimensionnel -1376 particules-
L'irréversibilité numérique du billard bidimensionnel -1376 particules- Visualisation bidimensionnelle des erreurs d'arrondi dans le calcul de la dynamique de Verhulst
Visualisation bidimensionnelle des erreurs d'arrondi dans le calcul de la dynamique de Verhulst Rotation autour de l'axe X de l'attracteur de Lorenz
Rotation autour de l'axe X de l'attracteur de Lorenz L'attracteur de Lorenz -sensibilité aux conditions initiales (la Rouge, la Verte et la Bleue)-
L'attracteur de Lorenz -sensibilité aux conditions initiales (la Rouge, la Verte et la Bleue)- L'attracteur de Lorenz -sensibilité à la méthode d'intégration utilisée (Rouge=Euler, Vert=Runge-Kutta/second ordre, Bleu=Runge-Kutta/quatrième ordre)-
L'attracteur de Lorenz -sensibilité à la méthode d'intégration utilisée (Rouge=Euler, Vert=Runge-Kutta/second ordre, Bleu=Runge-Kutta/quatrième ordre)- Calcul de l'attracteur de Lorenz sur trois ordinateurs différents (le Rouge, le Vert et le Bleu : sensibilité aux erreurs d'arrondi)
Calcul de l'attracteur de Lorenz sur trois ordinateurs différents (le Rouge, le Vert et le Bleu : sensibilité aux erreurs d'arrondi) Rotation autour de l'axe X de l'attracteur de Lorenz (1000 itérations), calculée sur deux ordinateurs différents
Rotation autour de l'axe X de l'attracteur de Lorenz (1000 itérations), calculée sur deux ordinateurs différents Rotation autour de l'axe X de l'attracteur de Lorenz (5000 itérations), calculée sur deux ordinateurs différents
Rotation autour de l'axe X de l'attracteur de Lorenz (5000 itérations), calculée sur deux ordinateurs différents Intégration du problème des N-corps (N=4 : une étoile, une planète lourde et une planète légère avec un satellite) calculé avec 2 options d'optimisation différentes (sensibilité aux erreurs d'arrondi)
Intégration du problème des N-corps (N=4 : une étoile, une planète lourde et une planète légère avec un satellite) calculé avec 2 options d'optimisation différentes (sensibilité aux erreurs d'arrondi) , il
s'agit, dans le contexte de l'Expérimentation Virtuelle, de montrer bien souvent des objets
sans image, soit qu'ils n'existent pas dans la
nature (tel cet ensemble de Julia dans les quaternions
, il
s'agit, dans le contexte de l'Expérimentation Virtuelle, de montrer bien souvent des objets
sans image, soit qu'ils n'existent pas dans la
nature (tel cet ensemble de Julia dans les quaternions  ),
soit que, bien qu'étant
naturels, il soit impossible, voire interdit, de
les représenter (comme l'atome d'hydrogène
),
soit que, bien qu'étant
naturels, il soit impossible, voire interdit, de
les représenter (comme l'atome d'hydrogène  ) ou encore
tout simplement parce qu'ils n'ont pas
d'équivalents visuels (une pression ou une
température par exemple...). S'il est clair
que montrer un objet à quatre dimensions
est chose difficile (tel
) ou encore
tout simplement parce qu'ils n'ont pas
d'équivalents visuels (une pression ou une
température par exemple...). S'il est clair
que montrer un objet à quatre dimensions
est chose difficile (tel  ), il est
malheureusement moins évident que toute
tentative de représentation, dans ce
domaine, est délicate. La difficulte vient
bien entendu des espaces, en général non
naturels, dans lesquels résident ces objets,
mais surtout de la non unicité des images
que l'on peut en donner : même dans les cas
les plus simples, des ambiguités et des
contradictions peuvent surgir. En toute généralite,
il n'y a pas unicité de la représentation.
), il est
malheureusement moins évident que toute
tentative de représentation, dans ce
domaine, est délicate. La difficulte vient
bien entendu des espaces, en général non
naturels, dans lesquels résident ces objets,
mais surtout de la non unicité des images
que l'on peut en donner : même dans les cas
les plus simples, des ambiguités et des
contradictions peuvent surgir. En toute généralite,
il n'y a pas unicité de la représentation.
 nous
montrent le même ensemble bidimensionnel (un "tableau") de nombres, la
seule différence se situant dans le code des couleurs
utilisées. En effet, pour obtenir ce type de représentation, il
suffit d'associer aux nombres (ou plus généralement à des
plages de valeurs numériques) des couleurs (en appelant aussi
couleur, par abus de langage, le noir, les gris et le blanc) ;
par exemple, il sera décide arbitrairement de représenter par
du rouge les points associés à des valeurs numériques
comprises entre 1.37 et 3.62. De cet arbitraire naissent les
difficultés ici presentées. De toute évidence, dans cet exemple, la perception
varie fortement d'une image à l'autre, les conclusions
possibles sur l'unique tableau de nombres sous-jacent
pouvant même être en contradiction les unes avec les autres !
Ces quatre représentations peuvent être qualifiées d'orthogonales...
Une sémiologie de la Visualisation Scientifique reste à créer ;
elle serait un lieu de rencontre privilégié entre les artistes et
les scientifiques.
nous
montrent le même ensemble bidimensionnel (un "tableau") de nombres, la
seule différence se situant dans le code des couleurs
utilisées. En effet, pour obtenir ce type de représentation, il
suffit d'associer aux nombres (ou plus généralement à des
plages de valeurs numériques) des couleurs (en appelant aussi
couleur, par abus de langage, le noir, les gris et le blanc) ;
par exemple, il sera décide arbitrairement de représenter par
du rouge les points associés à des valeurs numériques
comprises entre 1.37 et 3.62. De cet arbitraire naissent les
difficultés ici presentées. De toute évidence, dans cet exemple, la perception
varie fortement d'une image à l'autre, les conclusions
possibles sur l'unique tableau de nombres sous-jacent
pouvant même être en contradiction les unes avec les autres !
Ces quatre représentations peuvent être qualifiées d'orthogonales...
Une sémiologie de la Visualisation Scientifique reste à créer ;
elle serait un lieu de rencontre privilégié entre les artistes et
les scientifiques.
 2 carrés gris identiques se déplaçant au-dessus d'une échelle de gris
2 carrés gris identiques se déplaçant au-dessus d'une échelle de gris Points noirs (à l'intérieur de carrés blancs aléatoires) sur un réseau carré
Points noirs (à l'intérieur de carrés blancs aléatoires) sur un réseau carré L'illusion de Zollner
L'illusion de Zollner Tas ou trou (vue aérienne) ?
Tas ou trou (vue aérienne) ? ).
).