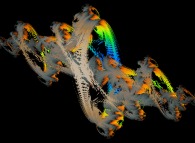
A foggy pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(0,1,0,0,0,0,0,0) -tridimensional cross-section-. |

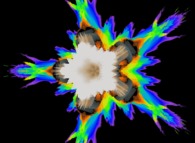
A foggy pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.58...,+0.63...,0,0,0,0,0,0) -tridimensional cross-section-. |

A foggy pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.58...,+0.63...,0,0,0,0,0,0) -tridimensional cross-section-. |

A foggy pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.58...,+0.63...,0,0,0,0,0,0) -tridimensional cross-section-. |

A foggy pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.58...,+0.63...,0,0,0,0,0,0) with a rotation about the X axis -tridimensional cross-section-. |

Pi/2 rotation about the X axis of a pseudo-quaternionic Julia set ('MandelBulb' like: a 'JuliaBulb') -tridimensional cross-section-. |

Close-up on a foggy pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.58...,+0.63...,0,0,0,0,0,0) with a rotation about the X axis -tridimensional cross-section-. |

A foggy pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.58...,+0.63...,0,0,0,0,0,0) with a rotation about the X axis -tridimensional cross-section-. |

A foggy pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.58...,+0.63...,0,0,0,0,0,0) with a rotation about the X axis -tridimensional cross-section-. |

A foggy pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.58...,+0.63...,0,0,0,0,0,0) -tridimensional cross-section-. |

A foggy pseudo-octonionic Julia set ('MandelBulb' like: a 'JuliaBulb') computed with A=(-0.58...,+0.63...,0,0,0,0,0,0) -tridimensional cross-section-. |