click to view the MPEG movie (cliquez pour voir le film MPEG)

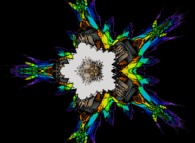
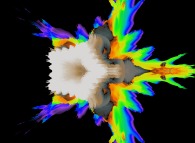
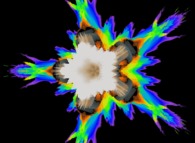
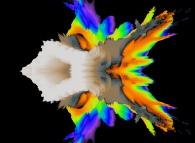
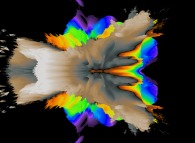
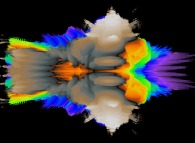
2.pi rotation about the Y axis of a pseudo-quaternionic Mandelbrot set (a 'MandelBulb') -tridimensional cross-section- [Rotation de 2.pi autour de l'axe Y d'un ensemble de Mandelbrot dans l'ensemble des pseudo-quaternions (un 'MandelBulb') -section tridimensionnelle-].




See the sixteen points of view:

A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section-  
A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section-  
A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section-  
A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section-


See the sixteen points of view (without black edges):

A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section-  
A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section-  
A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section-  
A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section- A pseudo-quaternionic Mandelbrot set (a 'MandelBulb')-tridimensional cross-section-


[for more information about pseudo-quaternionic numbers (en français/in french)]
[for more information about pseudo-octionic numbers (en français/in french)]

[for more information about N-Dimensional Deterministic Fractal Sets (in english/en anglais)]
[Plus d'informations à propos des Ensembles Fractals Déterministes N-Dimensionnels (en français/in french)]


(CMAP28 WWW site: this page was created on 12/01/2009 and last updated on 05/12/2021 19:06:43 -CEST-)



[See the generator of this picture [Voir le générateur de cette image]]

[See all related pictures (including this one) [Voir toutes les images associées (incluant celle-ci)]]

[See the following comment(s): quaternionic numbers, pseudo-quaternionic numbers, Mandelbrot set [Voir le(s) commentaire(s) suivant(s): quaternions, pseudo-quaternions, ensemble de Mandelbrot]]
[Please visit the related DeterministicFractalGeometry picture gallery [Visitez la galerie d'images DeterministicFractalGeometry associée]]

[Go back to AVirtualMachineForExploringSpaceTimeAndBeyond [Retour à AVirtualMachineForExploringSpaceTimeAndBeyond]]

[The Y2K Bug [Le bug de l'an 2000]]

[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[Mail [Courrier]]
[About Pictures and Animations [A Propos des Images et des Animations]]


Copyright © Jean-François Colonna, 2009-2021.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / Ecole Polytechnique, 2009-2021.