Courbes de Hilbert et Nœuds Infinis
CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[N'oubliez pas de visiter Une Machine Virtuelle à Explorer l'Espace-Temps et au-delà où vous trouverez plus de 10.000 images et animations à la frontière de l'Art et de la Science]
(Site WWW CMAP28 : cette page a été créée le 16/05/2022 et mise à jour le 16/01/2025 11:27:17 -CET-)
[in english/en anglais]
En 1890 Giuseppe Peano découvrit des courbes passant par tous les points d'un carré (et d'un cube) mettant
ainsi en évidence des surjections continues entre [0,1] et [0,1]x[0,1] (et [0,1]x[0,1]x[0,1]).
Au cours des années suivantes, David Hilbert définit d'autres telles courbes qui peuvent être generalisées.
Les courbes de Hilbert bidimensionnelles :
Soit C1(T)
une courbe paramétrique  définie à l'aide de 2 fonctions réelles de T
(T ∈ [0,1])
X1(T) ∈ [0,1] et Y1(T) ∈ [0,1]
telles que
:
définie à l'aide de 2 fonctions réelles de T
(T ∈ [0,1])
X1(T) ∈ [0,1] et Y1(T) ∈ [0,1]
telles que
:
X1(T=0)=0 Y1(T=0)=0 (coin en bas et à gauche)
X1(T=1)=1 Y1(T=1)=0 (coin en bas et à droite)
On définit ensuite une suite de courbes Ci(T) (i >= 1) de la façon suivante
:
Ci(T) = {Xi(T),Yi(T)} ∈ [0,1]x[0,1] --> Ci+1(T) = {Xi+1(T),Yi+1(T)} ∈ [0,1]x[0,1]
if T ∈ [0,1/4[ :
Xi+1(T) = Yi(4T-0)
Yi+1(T) = Xi(4T-0)
Transformation 1
if T ∈ [1/4,2/4[ :
Xi+1(T) = Xi(4T-1)
Yi+1(T) = 1+Yi(4T-1)
Transformation 2
if T ∈ [2/4,3/4[ :
Xi+1(T) = 1+Xi(4T-2)
Yi+1(T) = 1+Yi(4T-2)
Transformation 3
if T ∈ [3/4,1] :
Xi+1(T) = 2-Yi(4T-3)
Yi+1(T) = 1-Xi(4T-3)
Transformation 4
Il convient de noter que 4=2d où d=2 est la dimension de l'espace.
Voir une courbe C1(T)  spéciale afin de comprendre la signification géométrique des 4 transformations
spéciale afin de comprendre la signification géométrique des 4 transformations  et de leur ordre
et de leur ordre  .
.
Voici les cinq premières courbes bidimensionnelles de Hilbert avec un nombre croissant d'itérations
:




 [Voir les couleurs utilisées pour visualiser le paramètre T]
[Voir les couleurs utilisées pour visualiser le paramètre T]
Voir la construction de quelques unes d'entre-d'elles
:





Voici quelques exemples de courbes bidimensionnelles de type Hilbert utilisant des courbes génératrices différentes
:






























Voici le "mapping" de quelques images à l'aide d'une courbe bidimensionnelle de Hilbert :
:
 | ==>
[itération 11] |  |
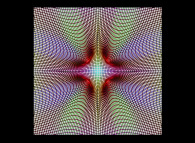 | ==>
[itération 10] |  |
 | ==>
[itération 9] |  |
 | ==>
[itération 10] |  |
Les courbes de Hilbert tridimensionnelles :
Soit C1(T)
une courbe paramétrique  définie à l'aide de 3 fonctions réelles de T
(T ∈ [0,1])
X1(T) ∈ [0,1], Y1(T) ∈ [0,1] et Z1(T) ∈ [0,1]
telles que
:
définie à l'aide de 3 fonctions réelles de T
(T ∈ [0,1])
X1(T) ∈ [0,1], Y1(T) ∈ [0,1] et Z1(T) ∈ [0,1]
telles que
:
X1(T=0)=0 Y1(T=0)=0 Z1(T=0)=0 (coin en bas et à gauche au premier plan)
X1(T=1)=1 Y1(T=1)=0 Z1(T=1)=0 (coin en bas et à droite au premier plan)
On définit ensuite une suite de courbes Ci(T) (i >= 1) de la façon suivante
:
Ci(T) = {Xi(T),Yi(T),Zi(T)} ∈ [0,1]x[0,1]x[0,1] --> Ci+1(T) = {Xi+1(T),Yi+1(T),Zi+1(T)} ∈ [0,1]x[0,1]x[0,1]
if T ∈ [0,1/8[ :
Xi+1(T) = Xi(8T-0)
Yi+1(T) = Zi(8T-0)
Zi+1(T) = Yi(8T-0)
Transformation 1
if T ∈ [1/8,2/8[ :
Xi+1(T) = Zi(8T-1)
Yi+1(T) = 1+Yi(8T-1)
Zi+1(T) = Xi(8T-1)
Transformation 2
if T ∈ [2/8,3/8[ :
Xi+1(T) = 1+Xi(8T-2)
Yi+1(T) = 1+Yi(8T-2)
Zi+1(T) = Zi(8T-2)
Transformation 3
if T ∈ [3/8,4/8[ :
Xi+1(T) = 1+Zi(8T-3)
Yi+1(T) = 1-Xi(8T-3)
Zi+1(T) = 1-Yi(8T-3)
Transformation 4
if T ∈ [4/8,5/8[ :
Xi+1(T) = 2-Zi(8T-4)
Yi+1(T) = 1-Xi(8T-4)
Zi+1(T) = 1+Yi(8T-4)
Transformation 5
if T ∈ [5/8,6/8[ :
Xi+1(T) = 1+Xi(8T-5)
Yi+1(T) = 1+Yi(8T-5)
Zi+1(T) = 1+Zi(8T-5)
Transformation 6
if T ∈ [6/8,7/8[ :
Xi+1(T) = 1-Zi(8T-6)
Yi+1(T) = 1+Yi(8T-6)
Zi+1(T) = 2-Xi(8T-6)
Transformation 7
if T ∈ [7/8,1] :
Xi+1(T) = Xi(8T-7)
Yi+1(T) = 1-Zi(8T-7)
Zi+1(T) = 2-Yi(8T-7)
Transformation 8
Il convient de noter que 8=2d où d=3 est la dimension de l'espace.
Voir une courbe C1(T)  spéciale afin de comprendre la signification géométrique des 8 transformations
spéciale afin de comprendre la signification géométrique des 8 transformations  et de leur ordre
et de leur ordre  .
.
Voici les quatre premières courbes tridimensionnelles de Hilbert avec un nombre croissant d'itérations
:



 [Voir les couleurs utilisées pour visualiser le paramètre T]
[Voir les couleurs utilisées pour visualiser le paramètre T]
Voir la construction de l'une d'elles
:




Voici quelques exemples de courbes tridimensionnelles de type Hilbert utilisant des courbes génératrices différentes et
en particulier des nœuds "ouverts"
:
































[More information about Peano Curves and Infinite Knots -in english/en anglais-]
[Plus d'informations à propos des Courbes de Peano et des Nœuds Infinis -en français/in french-]
Les nœuds infinis :
Nota :
Un nœud mathématique est une courbe fermée mais pour en faire une courbe de type C1(T) il est nécessaire de l'ouvrir
(par soucis de lisibilité, les deux extrémités "libres" des courbes Ci(T) ne seront donc pas connectées : il s'agit
des sommets du cube au premier plan, en bas, à gauche et à droite respectivement visualisés comme de plus grosses sphères...).
Utilisons un nœud 3-trèfle  comme courbe paramétrique C1(T) et ouvrons-le
comme courbe paramétrique C1(T) et ouvrons-le  .
.
Voici les cinq premières courbes
Ci(T) (i ∈ [1,5]) :




 Voir la palette de couleurs utilisée pour visualiser le paramètre T.
Voir la palette de couleurs utilisée pour visualiser le paramètre T.
Après un nombre infini d'itérations, la courbe remplit le cube [0,1]x[0,1]x[0,1] : c'est un premier "nœud infini"...
Maintenant, utilisons un nœud 5-trèfle  comme courbe paramétrique C1(T) et ouvrons-le
comme courbe paramétrique C1(T) et ouvrons-le  .
.
Voici les cinq premières courbes
Ci(T) (i ∈ [1,5])
donnant après un nombre infini d'itérations un deuxième "nœud infini"
:




 Voir la palette de couleurs utilisée pour visualiser le paramètre T.
Voir la palette de couleurs utilisée pour visualiser le paramètre T.
Maintenant, utilisons un nœud 7-trèfle  comme courbe paramétrique C1(T) et ouvrons-le
comme courbe paramétrique C1(T) et ouvrons-le  .
.
Voici les cinq premières courbes
Ci(T) (i ∈ [1,5])
donnant après un nombre infini d'itérations un troisième "nœud infini"
:




 Voir la palette de couleurs utilisée pour visualiser le paramètre T.
Voir la palette de couleurs utilisée pour visualiser le paramètre T.
Enfin, il est evidemment possible de remplir des
variétés tridimensionelles plus "complexes" qu'un cube et par exemple :
| Variété tridimensionnelle | ==> | Courbe C | ==> | Nœud remplissant la variété tridimensionnelle |
Copyright © Jean-François COLONNA, 2022-2025.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2022-2025.

 définie à l'aide de 2 fonctions réelles de T
(T ∈ [0,1])
X1(T) ∈ [0,1] et Y1(T) ∈ [0,1]
telles que
:
définie à l'aide de 2 fonctions réelles de T
(T ∈ [0,1])
X1(T) ∈ [0,1] et Y1(T) ∈ [0,1]
telles que
:
 spéciale afin de comprendre la signification géométrique des 4 transformations
spéciale afin de comprendre la signification géométrique des 4 transformations  et de leur ordre
et de leur ordre  .
.



 [Voir les couleurs utilisées pour visualiser le paramètre T]
[Voir les couleurs utilisées pour visualiser le paramètre T]








































 définie à l'aide de 3 fonctions réelles de T
(T ∈ [0,1])
X1(T) ∈ [0,1], Y1(T) ∈ [0,1] et Z1(T) ∈ [0,1]
telles que
:
définie à l'aide de 3 fonctions réelles de T
(T ∈ [0,1])
X1(T) ∈ [0,1], Y1(T) ∈ [0,1] et Z1(T) ∈ [0,1]
telles que
:
 spéciale afin de comprendre la signification géométrique des 8 transformations
spéciale afin de comprendre la signification géométrique des 8 transformations  et de leur ordre
et de leur ordre  .
.


 [Voir les couleurs utilisées pour visualiser le paramètre T]
[Voir les couleurs utilisées pour visualiser le paramètre T]




























 comme courbe paramétrique C1(T) et ouvrons-le
comme courbe paramétrique C1(T) et ouvrons-le  Voir la palette de couleurs utilisée pour visualiser le paramètre T.
Voir la palette de couleurs utilisée pour visualiser le paramètre T.
 comme courbe paramétrique C1(T) et ouvrons-le
comme courbe paramétrique C1(T) et ouvrons-le  Voir la palette de couleurs utilisée pour visualiser le paramètre T.
Voir la palette de couleurs utilisée pour visualiser le paramètre T.
 comme courbe paramétrique C1(T) et ouvrons-le
comme courbe paramétrique C1(T) et ouvrons-le  Voir la palette de couleurs utilisée pour visualiser le paramètre T.
Voir la palette de couleurs utilisée pour visualiser le paramètre T.





