The first four iterations of the construction of the von Koch snowflake
[Le flocon de von Koch s'obtient en partant d'un triangle équilatéral. Chacun de ses côtés est remplacé par une figure faite de quatre segments trois fois plus petits. Ce processus est ensuite itéré indéfiniment (4 fois sur cette image).]. | 
The Sierpinski Carpet -iteration 1 to 5-
[Le tapis de Sierpinski s'obtient en partant d'un carré que l'on découpe en 3x3 petits carrés, puis en supprimant celui qui est au centre et enfin en itérant ce processus indéfiniment (5 fois sur cette image). L'objet obtenu a une dimension fractale égale à log(8)/log(3)=1.8927...]. | 
The Menger Sponge -iteration 5-
[L'éponge de Menger s'obtient en partant d'un cube que l'on découpe en 3x3x3 petits cubes, puis en supprimant les sept qui sont au centre ainsi qu'au milieu des six faces et enfin en itérant ce processus indéfiniment (5 fois sur cette image). L'objet obtenu a une dimension fractale égale à log(20)/log(3)=2.7268...]. | 
Bidimensional Hilbert Curve -iterations 1 to 5-
[Lors de ses travaux sur les infinis, Georg Cantor a démontré que R, R2, R3,... avaient le même cardinal. Cela a ouvert la porte aux courbes passant par tous les points d'un carré. Cette image montre 5 itérations du processus de construction d'une telle courbe due a Hilbert]. | 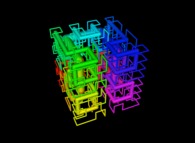
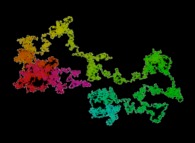
Tridimensional Hilbert Curve -iterations 1 to 3-
[Lors de ses travaux sur les infinis, Georg Cantor a démontré que R, R2, R3,... avaient le même cardinal. Cela a ouvert la porte aux courbes passant par tous les points d'un cube. Cette image montre 3 itérations du processus de construction d'une telle courbe due a Hilbert]. |
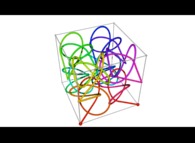
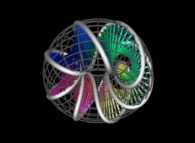
A Tridimensional Hilbert-like Curve base on an 'open' 3-foil torus knot -iteration 2-
[Lors de ses travaux sur les infinis, Georg Cantor a démontré que R, R2, R3,... avaient le même cardinal. Cela a ouvert la porte aux courbes passant par tous les points d'un cube. Cette image montre 2 itérations du processus de construction d'une telle courbe basé sur un nœud de trèfle 'ouvert']. | 
A sphere described by means of a Bidimensional Hilbert Curve -iteration 7-
[Lors de ses travaux sur les infinis, Georg Cantor a démontré que R, R2, R3,... avaient le même cardinal. Cela a ouvert la porte aux courbes passant par tous les points d'un carré. Cette sphère est construite en parcourant son espace de paramétrage {u,v} le long d'une telle courbe due a Hilbert]. | 
The Klein bottle described by means of a Bidimensional Hilbert Curve -iteration 7-
[Lors de ses travaux sur les infinis, Georg Cantor a démontré que R, R2, R3,... avaient le même cardinal. Cela a ouvert la porte aux courbes passant par tous les points d'un carré. Cette bouteille de Klein est construite en parcourant son espace de paramétrage {u,v} le long d'une telle courbe due a Hilbert]. | 
A Ball described by means of a Tridimensional Hilbert Curve -iteration 4-
[Lors de ses travaux sur les infinis, Georg Cantor a démontré que R, R2, R3,... avaient le même cardinal. Cela a ouvert la porte aux courbes passant par tous les points d'un cube. Cette boule est construite en parcourant son espace de paramétrage {u,v,w} le long d'une telle courbe due a Hilbert]. | 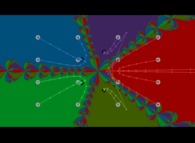
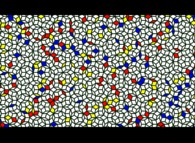
Visualization of the Newton's method when computing the roots of Z5=1
[Les racines N-ièmes de l'unité sont triviales à calculer exactement. Mais il est possible aussi de le faire via la méthode itérative de Newton. Le plan complexe se partionne alors en N zones de structures fractales correspondant aux N racines (N=5 dans cet exemple qui montre quelques trajectoires menant de 16 points -disques blancs- aux 5 racines -carrés noirs-)]. |
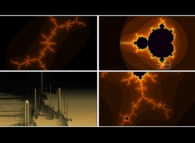
Along the border of the Mandelbrot set
[L'ensemble de Mandelbrot M est l'ensemble des nombres complexes définissant des ensembles de Julia J connexes. Cette image est extraite d'une animation présentant un voyage le long de la frontière de M et les J correspondant au point courant. La troisième dimension visualise le nombre d'itérations effectuées lors du calcul de M]. | 
A foggy pseudo-quaternionic Mandelbrot set (a 'MandelBulb') -tridimensional cross-section-
[Un ensemble de Mandelbrot calculé dans l'ensemble des 'pseudo-quaternions' qui utilise une arithmétique différente de celles des quaternions]. | 
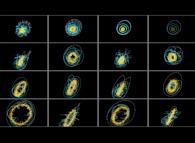
Tridimensional high resolution visualization of the Verhulst dynamics -'Time Ships', a Tribute to Stephen Baxter-
[La dynamique de Verhulst est définie par l'itération Xn=RXn-1(1-Xn-1). Pour R > 3.569 les valeurs de Xn sont chaotiques, sensibles aux conditions initiales et donc aux erreurs d'arrondi. En général, R est une constante, mais il est possible de modifier cette valeur en fonction de n. Dans cet exemple, l'espace est tridimensionnel. En chaque point de coordonnées {R1,R2,R3} l'itération de Verhulst utilisant X0=0.5 et un R fonction de {n,R1,R2,R3} va être étudiée via son exposant de Lyapunov: si elle est non chaotique, le point {R1,R2,R3} sera marqué avec une couleur fonction de {R1,R2,R3} et si elle est chaotique ce point restera vide.]. |


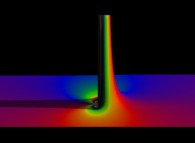
![Tridimensional display of the Riemann Zeta function inside [-50.0,+50.0]x[-50.0,+50.0] (bird's-eye view) Tridimensional display of the Riemann Zeta function inside [-50.0,+50.0]x[-50.0,+50.0] (bird's-eye view)](../images/ZETA.21.IdM.m.D/timbre.jpg)