Visualizing with Spheres






Jean-François COLONNA
[Contact me]

www.lactamme.polytechnique.fr

CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
france telecom, France Telecom R&D

[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[Please, visit A Virtual Machine for Exploring Space-Time and Beyond, the place where you can find more than 10.000 pictures and animations between Art and Science]
(CMAP28 WWW site: this page was created on 11/1/1996 and last updated on 10/03/2024 17:10:38 -CEST-)



Abstract: Computer plays today a key-role in Science. Picture synthesis is the only way to analyse the huge volume of results produced by Numerical Simulations. Unfortunately the objects displayed are far from those we experience in our everyday life. Choosing arbitrary shapes or again colors can lead us to erroneous analysis. In this short note we promote the use of one of the simplest geometric object as an almost universal neutral viualization medium.


Keywords: Scientific visualization, Numerical Simulation, Virtual Experimentation, Sphere.



Today, computers are omnipresent in our laboratories; in this short note I should like to focus on the so-called Numerical Simulation. Mathematics is the language used to write natural laws; equations studied by mathematicians and physicians are so complex that they cannot be solved without the help of computers. Speeds of more than one hundred mega-flops are common today and some of the fastest computers are close to reach the tera-flops level. Then we are able to produce huge amount of numerical results that, thanks to computers graphics, can be analysed in order to allow us a better understanding of the underlying laws.

I call this process (using together numerical simulation and picture synthesis), Virtual Experimentation [01]. Scientists are then faced with two major dangers (traps?):


This last point can be illustrated with what can be said to be the simplest case of Scientific Visualization: the one of a bidimensional scalar field. As a matter of fact, it is the simplest case because the display medium is bidimensional too (for example, a computer screen); then a trivial mapping exists between the numerical values and the picture and each {x,y} value can be visualized as a colored pixel. But an important question has to be answered: how to assign colors to each numerical value? To show there is unfortunately no unique answer, this picture uses four color palettes to visualize the same bidimensional scalar field; it displays four very different pictures; for example:


The conclusion we can draw from this is straightforward: in the field of scientific visualization, things must be kept as simple and as neutral as possible... I should like to extend this point of view with problems of a higher complexity.


Even if bidimensional scalar fields are of a great interest (see for example the so-called bidimensional fluid dynamics), our computers allow us today the study of much more complex spaces: bidimensional manifolds embedded in tridimensional spaces, tridimensional vector fields,... One of the simplest geometrical object, the sphere, can be there very useful and the use of spheres is already quite natural in a lot of problems.

A sphere can be defined with the following attributes:


Moreover, the sphere is one of the easiest graphical object to visualize...


Let's start with scalar mono- and bidimensional data. For the sphere paradigm to be helpful, we must sample these data; I call this process atomization. This process will give us a set of points; each of them will be visualized as a lighted sphere centered on it (by the way, these sets can be very far from our daily experiments; then, tridimensional clues must be given -like depth cueing or again fog effects, see [04]-). Its radius r and its {R,G,B} color are available to display a maximum of four different scalar values Vi where i ∈ [1,4] (for the sake of simplicity, it is assumed that Vi are non negative; if not, it suffices to apply appropriate linear transformations); this will help correlating different data sets. The four parameters r and {R,G,B} can be defined as follows: 
                    r = f (V )
                         r  i


                    R = f (V )
                         R  i


                    V = f (V )
                         V  i


                    B = f (V )
                         B  i
but it is strongly suggested to keep things as simple as possible in order to avoid misconstructions. Here are some straightforward advices:


As examples,the Lorenz attractor 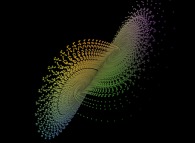is displayed using one sphere for each time step, when the atomization process for the Jeener surface 1 reveals the intricate inside details without the ambiguities of transparencies, when the apparent variation of sphere sizes (due to the projection) gives a good depth information.


All that have been said previously can be extended to scalar tridimensional data: spheres can be used to display voxels [05][06] As a matter of fact, the atomization process allows us to see through things without the ambiguities of transparencies (without forgetting the limits of this last process when there are to much levels of transparent sets). All that was said previously remains true; but in this case the ability to move around the scene, to penetrate inside it, is more than important. Then, when displaying time-dependent data, it is necessary to be careful because two time parameters have to be displayed simulteneously:

Except for entertainment purposes, it is suggested to freeze To during Td evolutions and inversely. One more time, things must be kept simple for a better understanding (let's recall there picture synthesis is used in this context as a scientific tool!). A tridimensional fractal field is a good example of this process.


All preceding advices were given for scalar data sets. In fact, spheres can be used to display non scalar data and for example vector fields. As a matter of fact, instead of using only one sphere for each data point, it is possible to use two or more aligned spheres to display a vector ; their attributes (ie. r and {R,G,B}) can be kept constant or not in order to exhibit gradient-like properties. It is straigthforward all this can be extended to much more complex structures.



Today, the discovery of rules for a fair use of Scientific Visualization must be a priority for everyone involved (software designers, engineers and scientists). Many decades ago it has been done for geographical maps, road signs,... and it works! In the scientific context, on the one hand we must never forget that there is no neutral tool and on the other hand we must define codes that will help to be bound toward what I shall call the Scientific Visualization Objectivity.






Copyright © Jean-François COLONNA, 1996-2024.
Copyright © France Telecom R&D and CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 1996-2024.