
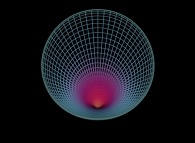
The 'hyperbolic cosine' of a sphere [Le 'cosinus hyperbolique' d'une sphère].

The 'hyperbolic cosine' of a sphere [Le 'cosinus hyperbolique' d'une sphère].
O --> O' = cosh(O)
 exponential |
 cosine |
 sine |
 tangent |
 hyperbolic cosine |
 hyperbolic sine |
 hyperbolic tangent |
 exponential |
 cosine |
 sine |
 tangent |
 hyperbolic cosine |
 hyperbolic sine |
 hyperbolic tangent |
