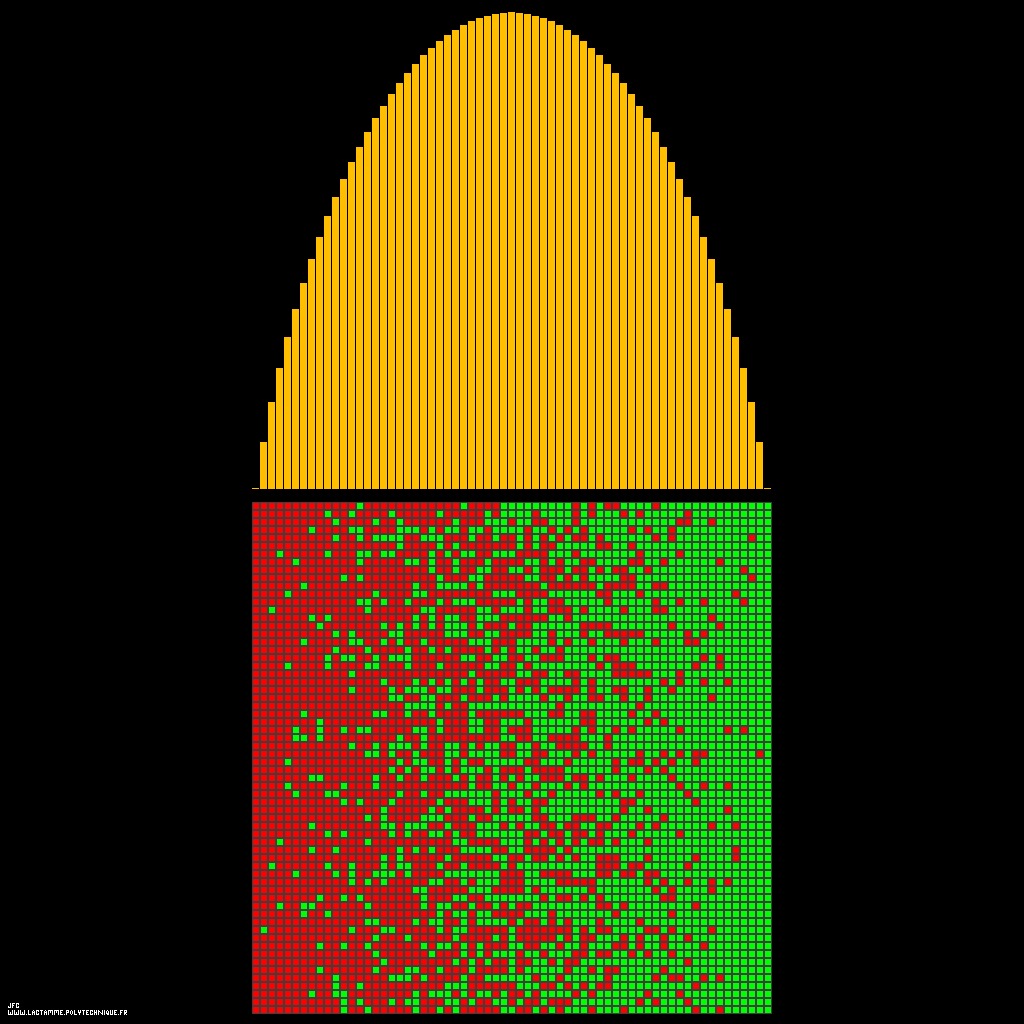
The configuration entropy of a set of n=64 particles [L'entropie de configuration d'un ensemble de n=64 particules].




E is a set containing n=64 (an arbitrary number -an even one in order to reach an unique maximum-) particles P. Each particle P has 2 sides: Head (red) and Tail (green). The displayed array has 64+1=65 columns. The columns are numbered with 'k' from 0 (left hand side) to 64 (right hand side). The column number k contains k 'Tail' particles and n-k 'Head' particles (the displayed configurations are generated at random). For each number k, there are C(n,k) different possible configurations with: 

                                 n!
                    C(n,k) = ----------
                              k!(n-k)!


                    n >= 0
                    k <= n


Here are the values of C(n,k) and log(C(n,k)) for each k: 

                    C(64,0)  = 1                              log(C(64,0))  =  0
                    C(64,1)  = 64                             log(C(64,1))  =  4.15
                    C(64,2)  = 2016                           log(C(64,2))  =  7.60
                    C(64,3)  = 41664                          log(C(64,3))  = 10.63
                    C(64,4)  = 635376                         log(C(64,4))  = 13.36
                    C(64,5)  = 7624512                        log(C(64,5))  = 15.84
                    C(64,6)  = 74974368                       log(C(64,6))  = 18.13
                    C(64,7)  = 621216192                      log(C(64,7))  = 20.24
                    C(64,8)  = 4426165368                     log(C(64,8))  = 22.21
                    C(64,9)  = 27540584512                    log(C(64,9))  = 24.03
                    C(64,10) = 151473214816                   log(C(64,10)) = 25.74
                    C(64,11) = 743595781824                   log(C(64,11)) = 27.33
                    C(64,12) = 3284214703056                  log(C(64,12)) = 28.82
                    C(64,13) = 13136858812224                 log(C(64,13)) = 30.20
                    C(64,14) = 47855699958816                 log(C(64,14)) = 31.49
                    C(64,15) = 159518999862720                log(C(64,15)) = 32.70
                    C(64,16) = 488526937079580                log(C(64,16)) = 33.82
                    C(64,17) = 1379370175283520               log(C(64,17)) = 34.86
                    C(64,18) = 3601688791018080               log(C(64,18)) = 35.82
                    C(64,19) = 8719878125622720               log(C(64,19)) = 36.70
                    C(64,20) = 19619725782651120              log(C(64,20)) = 37.51
                    C(64,21) = 41107996877935680              log(C(64,21)) = 38.25
                    C(64,22) = 80347448443237920              log(C(64,22)) = 38.92
                    C(64,23) = 146721427591999680             log(C(64,23)) = 39.52
                    C(64,24) = 250649105469666120             log(C(64,24)) = 40.06
                    C(64,25) = 401038568751465792             log(C(64,25)) = 40.53
                    C(64,26) = 601557853127198688             log(C(64,26)) = 40.93
                    C(64,27) = 846636978475316672             log(C(64,27)) = 41.28
                    C(64,28) = 1118770292985239888            log(C(64,28)) = 41.55
                    C(64,29) = 1388818294740297792            log(C(64,29)) = 41.77
                    C(64,30) = 1620288010530347424            log(C(64,30)) = 41.92
                    C(64,31) = 1777090076065542336            log(C(64,31)) = 42.02
 
                    C(64,32) = 1832624140942590534            log(C(64,32)) = 42.05
 
                    C(64,33) = 1777090076065542336            log(C(64,33)) = 42.02
                    C(64,34) = 1620288010530347424            log(C(64,34)) = 41.92
                    C(64,35) = 1388818294740297792            log(C(64,35)) = 41.77
                    C(64,36) = 1118770292985239888            log(C(64,36)) = 41.55
                    C(64,37) = 846636978475316672             log(C(64,37)) = 41.28
                    C(64,38) = 601557853127198688             log(C(64,38)) = 40.93
                    C(64,39) = 401038568751465792             log(C(64,39)) = 40.53
                    C(64,40) = 250649105469666120             log(C(64,40)) = 40.06
                    C(64,41) = 146721427591999680             log(C(64,41)) = 39.52
                    C(64,42) = 80347448443237920              log(C(64,42)) = 38.92
                    C(64,43) = 41107996877935680              log(C(64,43)) = 38.25
                    C(64,44) = 19619725782651120              log(C(64,44)) = 37.51
                    C(64,45) = 8719878125622720               log(C(64,45)) = 36.70
                    C(64,46) = 3601688791018080               log(C(64,46)) = 35.82
                    C(64,47) = 1379370175283520               log(C(64,47)) = 34.86
                    C(64,48) = 488526937079580                log(C(64,48)) = 33.82
                    C(64,49) = 159518999862720                log(C(64,49)) = 32.70
                    C(64,50) = 47855699958816                 log(C(64,50)) = 31.49
                    C(64,51) = 13136858812224                 log(C(64,51)) = 30.20
                    C(64,52) = 3284214703056                  log(C(64,52)) = 28.82
                    C(64,53) = 743595781824                   log(C(64,53)) = 27.33
                    C(64,54) = 151473214816                   log(C(64,54)) = 25.74
                    C(64,55) = 27540584512                    log(C(64,55)) = 24.03
                    C(64,56) = 4426165368                     log(C(64,56)) = 22.21
                    C(64,57) = 621216192                      log(C(64,57)) = 20.24
                    C(64,58) = 74974368                       log(C(64,58)) = 18.13
                    C(64,59) = 7624512                        log(C(64,59)) = 15.84
                    C(64,60) = 635376                         log(C(64,60)) = 13.36
                    C(64,61) = 41664                          log(C(64,61)) = 10.63
                    C(64,62) = 2016                           log(C(64,62)) =  7.60
                    C(64,63) = 64                             log(C(64,63)) =  4.15
                    C(64,64) = 1                              log(C(64,64)) =  0


The configuration entropy S is defined as: 
                    S = K.log(N)
K being the Boltzmann constant: 
                                  -23
                    K = 1.38066x10
and: 
                    N=C(n,k)


For this n-particle system, the configuration entropy is displayed as an orange histogram for each k. Its maximum is reached when there is the same number of Head particles and Tail ones; then n-k=k (n being an even number).


(CMAP28 WWW site: this page was created on 08/20/2021 and last updated on 12/30/2021 17:55:19 -CET-)



[See the generator of this picture [Voir le générateur de cette image]]

[See all related pictures (including this one) [Voir toutes les images associées (incluant celle-ci)]]

[Please visit the related ImagesDidactiques picture gallery [Visitez la galerie d'images ImagesDidactiques associée]]
[Please visit the related ParticleSystems picture gallery [Visitez la galerie d'images ParticleSystems associée]]

[Go back to AVirtualMachineForExploringSpaceTimeAndBeyond [Retour à AVirtualMachineForExploringSpaceTimeAndBeyond]]

[The Y2K Bug [Le bug de l'an 2000]]

[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[Mail [Courrier]]
[About Pictures and Animations [A Propos des Images et des Animations]]


Copyright © Jean-François Colonna, 2021-2021.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / Ecole Polytechnique, 2021-2021.