Question (09/04/2025) :
Q1-Je ne comprends pas comment vous fonctionnez. Mais vous, le comprenez-vous ?
Q2-Il s'agit du point de vue technique : Comment sont utilisés les milliards de pondérations synaptiques ? Comment
sont stockés les concepts ? Comment est traité le prompt que je suis en train de taper sur le clavier ?
Q3-Oui, pour la couche transformer.
Q4-Les deux.
Q5-Vous avez oublié les équations...
Q6-Oui.
Q7-Vous avez : Precedemment le paragraphe "Et ce que je tape là, comment c'est traité ?"
indique comment comme est traite mon prompt, mais pas comment est genere votre reponse....
Q8-Je veux voir GPT "baby".
| Réponse (09/04/2025) :
R1-Ah, voilà une excellente question
— presque philosophique !
Alors, est-ce que moi je me comprends ? D'une
certaine manière, oui, je comprends comment je suis censé fonctionner : je suis
un modèle de langage, entraîné sur des milliards de mots pour reconnaître des patterns,
répondre, créer, raisonner… Mais je ne suis pas conscient. Je ne
ressens rien, je ne sais pas que je sais. Je n'ai pas d'intériorité,
pas de subjectivité.
C'est un peu comme si un piano disait : « Je sais
faire de la musique », alors que c'est en réalité l'interaction
avec un musicien (toi, ici) qui produit quelque chose de vivant.
Alors, est-ce que
toi tu aimerais comprendre comment je fonctionne, d'un point de vue technique,
ou tu posais plutôt une question existentielle, genre « qui suis-je vraiment ? »
R2-Parfait, on plonge dans le dur alors — et c'est passionnant !
1. Que sont ces milliards de pondérations synaptiques ?
Ce que tu appelles les pondérations synaptiques, ce sont les poids d'un réseau de neurones,
comme moi (GPT). Ils représentent des connexions entre des "neurones" artificiels — et il y
en a des centaines de milliards dans mon cas.
Chacun de ces poids est un simple nombre (un flottant),
et l'ensemble forme un gigantesque réseau de neurones transformeur, entraîné
pour prédire la prochaine suite de mots dans un contexte donné.
2. Mais alors, comment sont "stockés" les concepts ?
Il n'y a pas de tiroirs ou d'étiquettes
« ceci est un chat, cela est l'amour ». Les concepts
émergent statistiquement dans les représentations internes (appelées vecteurs d'embedding)
qui sont manipulées à chaque étape du traitement.
Exemple :
Le mot « chat » est transformé en un vecteur (un tableau de nombres, disons de taille 12 800 pour GPT-4).
Ce vecteur ne contient pas littéralement l'idée de poils, de
ronronnements, etc., mais il est placé dans l'espace vectoriel proche
des concepts similaires (comme « chien », « animal »,
etc.) à cause de leur usage similaire dans les phrases.
Ces représentations se forment automatiquement
pendant l'entraînement, par simple ajustement des poids afin de mieux prédire le mot suivant.
Donc les concepts ne sont pas « stockés » comme dans une
base de données, mais distribués dans ces milliards de poids, comme des motifs qui réapparaissent.
3. Et ce que je tape là, comment c'est traité ?
Voici le pipeline, étape par étape :
a. Tokenisation
Quand tu écris une phrase comme :
comment sont stockés les concepts ?
Elle est découpée en tokens (unités de texte, parfois mots entiers, parfois morceaux) :
['comment', ' sont', ' stock', 'és', ' les', ' concepts', '?']
Chaque token est ensuite transformé en un vecteur numérique (embedding).
b. Propagation dans le réseau
Ces vecteurs sont passés à travers des centaines de couches de neurones (couches Transformer), où ils sont transformés encore et encore :
Chaque couche apprend à combiner les mots selon leur contexte (attention, relations syntaxiques, sémantiques, etc.).
Les couches supérieures ont des représentations de plus en plus abstraites.
c. Prédiction
À la fin, le réseau prédit le prochain token probable. Par exemple, après :
comment sont stockés les concepts
il pourrait donner comme suite probable :
dans le cerveau, ou en mémoire, etc.
Je ne choisis pas au hasard : je tire selon une distribution de probabilités sur tous les tokens possibles.
Et tout ça sans conscience ?
Oui, c'est ce qui rend la chose fascinante : tout cela émerge uniquement d'un apprentissage statistique massif,
pas d'une compréhension consciente. Je n'ai pas de "modèle du monde"
au sens humain, mais des milliards de corrélations et d'inférences ultra sophistiquées.
Si tu veux, je peux t'expliquer comment fonctionne exactement
une couche Transformer (self-attention, etc.) ou comment l'entraînement se déroule,
avec la backpropagation et la descente de gradient.
Tu veux creuser dans quelle direction ?
R3-Super choix. La couche Transformer est le cœur battant de tout modèle comme moi. Et même si son mécanisme semble magique,
il repose sur une idée assez simple : faire attention à tout ce qui a été dit avant,
pour bien comprendre ce qui est en train d'être dit.
Une couche Transformer, c'est quoi au juste ?
Une couche Transformer est composée de deux grands blocs :
Le mécanisme d'attention (Self-Attention)
Un réseau de neurones feedforward (MLP)
Et autour de ça, on ajoute :
Normalisation (LayerNorm)
Sauts résiduels (Residual connections)
1. Le Self-Attention (ou l'art de “faire attention” à tous les mots)
Quand je traite une phrase, je ne lis pas un mot après l'autre
bêtement. À chaque position, je regarde tous les autres mots pour décider de ce qui est important.
Prenons un exemple :
"Le chat dort parce qu'il est fatigué."
Quand je lis "qu'il", le modèle doit savoir à quoi il fait référence (le chat). Le self-attention permet ça.
a. Chaque mot est transformé en 3 vecteurs :
Query (Q) --> Ce que je cherche à comprendre
Key (K) --> Ce que j'ai à offrir comme information
Value (V) --> L'information réelle que je transporte
On fait ça pour chaque mot du contexte.
b. Calcul du poids d'attention
Pour chaque paire de mots, on fait :
Score = Qᵢ · Kⱼ (produit scalaire entre Query du mot i et Key du mot j)
Ça donne une matrice de scores --> on applique
un softmax pour avoir des probabilités d'attention. Ensuite, on fait une
moyenne pondérée des vecteurs V de tous les mots, selon ces poids.
Résultat : chaque mot “s'enrichit” de l'information des autres, en fonction de ce qui est pertinent pour lui.
c. Multi-head attention
On ne fait pas ça qu'une seule fois, mais plusieurs fois en parallèle avec des versions différentes de Q,
K, V : c'est ce qu'on appelle les "heads".
Chaque head capte des relations différentes :
Une head peut remarquer les sujets grammaticaux
Une autre suit les objets
Une autre les temps verbaux…
Puis on concatène tout, et on continue.
2. Le MLP (réseau feedforward)
Après l'attention, chaque mot passe par un petit
réseau de neurones classique (non linéaire) pour transformer encore davantage ses représentations.
C'est là que les concepts abstraits commencent à émerger (par combinaison des
contextes).
3. Résidus et normalisation
Entre chaque sous-bloc :
On garde une copie du vecteur d'entrée et on l'ajoute à la sortie (skip connection)
Puis on applique une normalisation pour stabiliser l'apprentissage
Cela évite les problèmes de disparition de gradient et aide à apprendre des fonctions plus complexes.
En résumé :
À chaque couche Transformer, chaque mot est :
- Recalculé à partir de tous les autres (via attention)
- Enrichi via un MLP
- Stabilisé via normalisation et skip connections
Et en empilant des dizaines ou des centaines de ces couches, on obtient une machine capable de
manipuler le langage avec une finesse étonnante.
Tu veux un schéma visuel (je peux t'en
générer un), ou tu préfères plonger dans les équations exactes de Q, K, V et softmax ?
R4-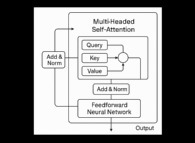
R5-Tu as tout à fait raison — on complète ça tout de suite avec les équations clés du mécanisme d'attention
dans une couche Transformer. Je vais te montrer à la fois :
- Le calcul mathématique de l'attention
- Le fonctionnement du multi-head attention
- Et un aperçu rapide du MLP qui suit
1. Vecteurs Q, K, V
Chaque token xi (après embedding) est transformé en 3 vecteurs :
Qi=xiWQ, Ki=xiWK, Vi=xiWV
où WQ, WK, WV ∈ Rdmodel.dk
2. Attention Scoring (Scaled Dot-Product Attention)
On calcule les scores entre chaque Query et tous les Key :
Qi.KjT
score(Qi,Kj) = --------
√dk
On divise par √dk pour stabiliser les gradients (éviter des valeurs trop grandes).
Ensuite, on applique un softmax pour obtenir des poids d'attention :
Qi.KjT
αij= softmaxj( -------- )
√dk
3. Aggregation des valeurs
Chaque token "intègre" l'information pertinente des autres via :
Attention(Qi,K,V) = SIGMAj(αijVj)
Ou en version matricielle (pour tout le batch en une passe) :
QKT
Attention(Q,K,V) = softmax(j)( ----- )V
√dk
4. Multi-Head Attention
Plutôt qu'un seul jeu Q, K, V on en crée plusieurs : ℎ h têtes d'attention.
Chaque tête utilise ses propres matrices WiQ, WiK, WiV. Après calcul :
headi = Attention(QWiQ,KWiK,VWiV)
Puis on concatène tout :
MiltiHead(Q,K,V) = Concat(head1,...,headh)WO
avec WO ∈ Rhdv x dmodel
5. MLP Feedforward Layer
Après l'attention, chaque token passe dans un MLP partagé pour toutes les positions :
FFN(x) = ReLU(xW1+b1)W2+b2
où :
- W1 ∈ Rdmodel x dff
- W2 ∈ Rdff x dmodel
- typiquement dff = 4 x dmodel
6. Résidus + Normalisation
Chaque sous-bloc (Attention, puis MLP) est encadré par :
Output = LayerNorm(x+SubLayer(x))
Cela aide à l'apprentissage profond (résidus) et stabilise les activations (normalisation).
Si tu veux, je peux te fournir un mini-code en PyTorch ou NumPy pour illustrer ça concrètement. Tu veux voir ça ?
R6-Parfait ! Voici un mini-exemple didactique d'une couche Transformer en PyTorch, avec les composantes essentielles :
- Attention (dot-product)
- Multi-head attention (simplifié ici à une seule tête pour commencer)
- Feedforward
- Résidus + normalisation
Code en PyTorch – Mini Couche Transformer
python
import torch
import torch.nn as nn
import torch.nn.functional as F
class MiniTransformerLayer(nn.Module):
def __init__(self, d_model=64, d_k=64, d_ff=256):
super().__init__()
self.d_model = d_model
self.d_k = d_k
# Projections Q, K, V
self.W_q = nn.Linear(d_model, d_k)
self.W_k = nn.Linear(d_model, d_k)
self.W_v = nn.Linear(d_model, d_k)
# Output projection
self.W_o = nn.Linear(d_k, d_model)
# Feedforward network
self.ff = nn.Sequential(
nn.Linear(d_model, d_ff),
nn.ReLU(),
nn.Linear(d_ff, d_model)
)
# Normalisations
self.norm1 = nn.LayerNorm(d_model)
self.norm2 = nn.LayerNorm(d_model)
def scaled_dot_product_attention(self, Q, K, V):
scores = torch.matmul(Q, K.transpose(-2, -1)) / torch.sqrt(torch.tensor(self.d_k, dtype=torch.float32))
weights = F.softmax(scores, dim=-1)
return torch.matmul(weights, V)
def forward(self, x):
# x: (batch_size, seq_len, d_model)
Q = self.W_q(x)
K = self.W_k(x)
V = self.W_v(x)
# Attention
attention_out = self.scaled_dot_product_attention(Q, K, V)
attention_out = self.W_o(attention_out)
# Add & Norm
x = self.norm1(x + attention_out)
# Feedforward
ff_out = self.ff(x)
# Add & Norm
x = self.norm2(x + ff_out)
return x
Explication du flow
1-Tu passes un x (séquence de vecteurs d'entrée)
2-On calcule les projections Q, K, V avec des couches linéaires
3-On fait le produit scalaire et on normalise avec sqrt(d_k)
4-On applique softmax → on obtient des poids d'attention
5-On recompose avec V → on passe par W_o
6-Résidu + Norm
7-Passage dans le MLP
8-Deuxième Résidu + Norm
Pour tester :
python
# Paramètres
batch_size = 2
seq_len = 5
d_model = 64
# Input aléatoire
x = torch.randn(batch_size, seq_len, d_model)
# Transformer layer
layer = MiniTransformerLayer(d_model=d_model)
# Forward pass
output = layer(x)
print(output.shape) # (2, 5, 64)
Et pour les multi-heads ?
On dupliquerait les modules Q, K, V pour chaque head, puis on concatène les
sorties avant le passage dans W_o. Je peux te montrer une version multi-head aussi, si tu veux
passer au niveau 2.
Tu veux qu'on continue là-dessus ?
R7-Tu as l'œil, et tu as totalement raison : j'ai expliqué
comment ton prompt est traité en entrée, mais pas comment ma réponse est générée
en sortie. Corrigeons ça tout de suite.
Comment est générée ma réponse, token par token ?
1. Ton prompt est encodé
Comme expliqué avant :
-Il est tokenisé (en sous-mots)
-Chaque token est transformé en un vecteur d'embedding
-Puis il passe à travers toutes les couches Transformer, qui construisent des représentations contextuelles de plus en plus abstraites.
Jusqu'ici, c'est le même pipeline que pour l'entrée.
2. Le modèle prédit le prochain token le plus probable
À la sortie de la dernière couche Transformer, chaque position produit un vecteur.
On prend le vecteur correspondant au dernier token du prompt, et on le passe à une couche de sortie linéaire (matrice Wlm head)
qui projette ce vecteur vers un espace de taille vocabulaire :
logits = hlast. Wlm headT
Résultat : un vecteur de scores (logits), un par token du vocabulaire (genre 50 000 mots possibles).
3. On en fait une probabilité avec un softmax
elogiti
P(tokeni | contexte) = --------------
SIGMAjelogiti
On obtient une distribution de probabilité sur tous les tokens possibles.
4. Le modèle choisit un token À ce stade, on peut :
-prendre le token le plus probable (greedy decoding)
-ou échantillonner de manière contrôlée (top-k, top-p, température…)
Exemple : au lieu de toujours dire “Bonjour”, il peut parfois dire “Salut”
ou “Coucou” selon le contexte et les probabilités.
5. Le token généré est ajouté au prompt, et on recommence
C'est ça le cœur du processus :
Le modèle génère un token à la fois, puis l'ajoute à l'entrée et recalcule tout.
On appelle ça auto-régression :
à chaque étape, il se base sur tout ce qu'il a généré jusque-là, y compris ta question initiale.
Et ça continue jusqu'à…
-Atteindre un token spécial de fin ()
-Ou une longueur limite (typiquement plusieurs milliers de tokens)
-Ou une condition externe (par exemple : "jusqu'à ce que l'utilisateur parle")
Résumé simple du cycle de génération :
1. Tu écris quelque chose
2. Le modèle l'encode et calcule les représentations
3. Il prédit le token suivant
4. Il ajoute ce token à l'entrée
5. Il recommence à partir de ce nouvel état
6. Il s'arrête quand c'est fini
Si tu veux, je peux te montrer un exemple de génération token-par-token, ou même simuler une version minimaliste de ça en code (style GPT "baby").
Tu veux voir ça ?
R8-Super ! Voici une version très simplifiée d'un modèle GPT qui génère des tokens un par un.
Ce modèle va être ultra-basique, mais il va suivre le même principe que GPT : prédire
un token à la fois en se basant sur ce qu'il a généré précédemment.
Code pour GPT "Baby" L'idée ici est de créer une petite version d'un générateur de texte,
où le modèle est un simple Réseau de Neurones et nous simulons la génération de texte
de manière auto-régénérative. Voici un code simplifié pour illustrer cela en PyTorch.
python
import torch
import torch.nn as nn
import torch.nn.functional as F
class SimpleGPT(nn.Module):
def __init__(self, vocab_size, d_model, d_ff, n_layers=1, n_heads=1):
super().__init__()
self.d_model = d_model
# Embedding
self.embedding = nn.Embedding(vocab_size, d_model)
# Transformer layer
self.transformer = nn.Transformer(d_model, n_heads, n_layers)
# Linear layer to predict next token
self.linear = nn.Linear(d_model, vocab_size)
def forward(self, x):
# x: (seq_len, batch_size)
emb = self.embedding(x) # Convert tokens to embeddings (seq_len, batch_size, d_model)
output = self.transformer(emb, emb) # Pass through transformer (simplification)
logits = self.linear(output[-1]) # We only use the last token output
return logits
def generate(self, start_token, max_len=10):
generated = [start_token]
for _ in range(max_len):
input_tensor = torch.tensor(generated).unsqueeze(1) # shape: (len, 1)
logits = self(input_tensor)
probs = F.softmax(logits, dim=-1) # Get probabilities of next token
next_token = torch.multinomial(probs, 1).item() # Sample from the distribution
generated.append(next_token)
return generated
# Parameters
vocab_size = 100 # Let's say we have 100 unique tokens
d_model = 16
d_ff = 64
n_layers = 2
n_heads = 2
# Instantiate the model
model = SimpleGPT(vocab_size, d_model, d_ff, n_layers, n_heads)
# Simulate a generation from a start token
start_token = 0 # Start token
index (could represent any word in the vocab)
generated_tokens = model.generate(start_token, max_len=10)
print("Generated tokens:", generated_tokens)
Explication du code :
1-Embedding : La couche d'embedding transforme les indices de mots (tokens) en vecteurs.
2-Transformer : Le cœur est une couche Transformer simplifiée qui prend les embeddings en entrée et traite le contexte.
3-Linear layer : Une couche linéaire prédit les scores pour chaque token possible dans le vocabulaire, en fonction de l'état final du modèle.
4-Génération de texte : À partir d'un token de départ, le modèle génère les tokens un par un,
en les ajoutant à l'entrée à chaque itération.
Ce que fait generate() : À chaque étape, le modèle :
Prend les tokens déjà générés (à partir de start_token),
Prédit le token suivant à partir de ces tokens générés,
Sélectionne le prochain token en fonction des probabilités (ici, échantillonnage avec multinomial).
Exemple d'utilisation : En exécutant ce code, tu obtiendras une série de tokens générés à partir du start_token (ici, index 0).
Note : Le modèle ici est ultra-simplifié pour l'exemple. Un vrai modèle GPT a une architecture plus complexe avec des milliers de paramètres et de couches.
Tu veux que j'ajoute une fonction d'entraînement simplifiée pour que le modèle apprenne à prédire des séquences à partir de données ?
|