![Click to download and possibly see the movie [Cliquez pour télécharger et voir éventuellement le film]](image.jpg "Click to download and possibly see the movie [Cliquez pour télécharger et voir éventuellement le film]")
Kasner billiard: Time-dependent billiard (from negative curvatures to positive curvature) with one accelerated particle [Billard de Kasner: Billard à géométrie variable (de courbures négatives à une courbure positive) avec une particule accélérée]
.
Kasner billiard: Time-dependent billiard (from negative curvatures to positive curvature) with one accelerated particle [Billard de Kasner: Billard à géométrie variable (de courbures négatives à une courbure positive) avec une particule accélérée]
.
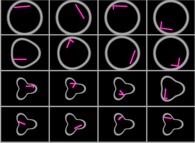
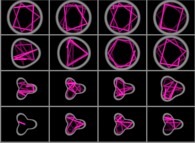
| En 1915, Albert Einstein publie la théorie de la Relativité Générale. Très rapidement de nombreux physiciens s'en emparent et
en particulier Georges Lemaître qui se rend compte alors que, malgré la croyance d'Albert Einstein, l'Univers ne pouvait
pas être statique. En 1929, les observations d'Edwin Hubble (en collaboration avec Milton Humason -ancien
muletier ayant travaillé à la construction de l'observatoire du Mont Wilson!-) et Vesto Melvin Slipher montrèrent que les autres galaxies
semblaient s'éloigner de nous, d'autant plus vite qu'elles étaient plus lointaines (cela se voit par une analyse
spectroscopique de leur lumière qui met alors en évidence un décalage vers le rouge des fréquences).
L'Univers n'était donc pas statique, mais en expansion et si l'on regarde "le film à l'envers", il doit donc montrer une contraction vers une "singularité" (de dimension nulle et de densité infinie -dans le cadre de la Relativité Générale-). Cette singularité fut surnommée "Big Bang" par Fred Hoyle dans les années 1950 pour dénigrer cette théorie préférant la sienne dite de l'état stationnaire, mais il dont il fut prouvé par la suite qu'elle n'était pas compatible avec les observations et mesures. Dans le cadre de la Relativité Générale, il semble pertinent de s'interroger sur les conditions initiales de ce "processus": mais peut-on y accéder? On notera que ne sachant toujours pas concilier Mécanique Quantique et gravitation, ce qui est suit est fort probablement approché, voire complètement faux... Les modèles dits "de Kasner" sont des solutions des équations d'Einstein pour un Univers homogène, anisotrope et sans matière. En particulier celui dit du "Mixmaster Universe" (du nom d'un appareil électroménager fabriqué par Sunbeam Products...) fut développé en 1969 par Charles Misner dans l'espoir de montrer que la "petite enfance" de l'Univers fut chaotique. Dans ce modèle, les tranches d'espace (à t constant) sont topolgiquement des sphères S3 qui peuvent se contracter, s'expanser mais aussi se distordre de façon anisotrope. Trois paramétres décrivent cette dynamique: un facteur d'échelle, ainsi que deux facteurs de forme. Charles Misner a montré que l'isotropie des sphères S3 n'était pas maintenue au cours de cette évolution et que cette dernière était au début chaotique pour ensuite évoluer vers de plus en plus d'ordre (nous sommes là pour en témoigner!). Mais en "remontant" le temps, il y a donc de plus en plus de chaos, ce qui empèche évidemment de connaître les conditions initiales! Ce modèle est tout à fait comparable à celui d'une boule qui rebondit sur les bords d'un billiard bimensionnel dont la forme évoluerait, au cours du temps, de concave à convexe. Ainsi, au début de son déplacement, la boule possède une trajectoire chaotique (comme l'Univers dans les premiers instants) pour arriver à une trajectoire périodique à la fin. Evidemment ces questions ne pourront trouver de réponses qu'en unifiant Relativité Générale et Mécanique Quantique, unification qui montrera peut-être que l'espace-temps est discontinu et constitué d'"atomes incompressibles" empéchant ainsi l'apparition d'une singularité... |