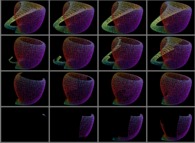
The Klein bottle described by means of a Bidimensional Hilbert Curve -iteration 7- [La bouteille de Klein décrite à l'aide d'une courbe de Hilbert bidimensionnelle -itération 7-].
The Klein bottle described by means of a Bidimensional Hilbert Curve -iteration 7- [La bouteille de Klein décrite à l'aide d'une courbe de Hilbert bidimensionnelle -itération 7-].
A la fin du dix-neuvième siècle, après que Georg Cantor ait montré que [0,1] et [0,1]x[0,1]
avait même cardinal, Giuseppe Peano puis David Hilbert ont proposé des courbes continues passant par tous les
points du carré unité.
Voici une grossière approximation de l'une d'elle:  obtenue à partir de la courbe génératrice  .
De nombreuses surfaces -variétés bidimensionnelles- dans un espace tridimensionnel peuvent être définies à l'aide d'un ensemble de trois fonctions: X = Fx(U,V) Y = Fy(U,V) Z = Fz(U,V)avec: U ∈ [Umin,Umax] V ∈ [Vmin,Vmax]Le carré unité [0,1]x[0,1] pouvant être rempli par une courbe continue, il est alors évident qu'il en est de même du rectangle [Umin,Umax]x[Vmin,Vmax] dans lequel sont définis les paramètres {U,V}. Et ainsi, en choisissant des couples {U,V} sur une telle courbe tracée dans le domaine de définition, la surface sera alors recouverte, elle-aussi, par une courbe remplissante. Due à Patrice Jeener, l'équation de la bouteille de Klein est la suivante: W(U,V) = 2.sin(U) + 3 Dx(U,V) = 4.cos(U) - 4.cos(2.U) Dy(U,V) = -12.sin(U) Rxy(U,V) = sqrt(Dx2(U,V) + Dy2(U,V)) Dy(U,V).W(U,V).cos(V)
Fx(U,V) = 4.sin(U) - 2.sin(2.U) - -----------------------
Rxy(U,V)
Dx(U,V).W(U,V).cos(V)
Fy(U,V) = 12.cos(U) + -----------------------
Rxy(U,V)
Fz(U,V) = W(U,V).sin(V)avec: U ∈ [0,2π] V ∈ [0,2π] [Plus d'informations sur ce sujet (en français/in french)] |
