De l'irrevérsibilité du temps numérique
CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641, École polytechnique, Institut Polytechnique de Paris, CNRS, France
[Site Map, Help and Search [Plan du Site, Aide et Recherche]]
[The Y2K Bug [Le bug de l'an 2000]]
[Real Numbers don't exist in Computers and Floating Point Computations aren't safe. [Les Nombres Réels n'existent pas dans les Ordinateurs et les Calculs Flottants ne sont pas sûrs.]]
[N'oubliez pas de visiter Une Machine Virtuelle à Explorer l'Espace-Temps et au-delà où vous trouverez plus de 10.000 images et animations à la frontière de l'Art et de la Science]
(Site WWW CMAP28 : cette page a été créée le 19/03/2025 et mise à jour le 25/03/2025 08:29:51 -CET-)
[in english/en anglais]
Mots-Clefs : Floating Point Numbers, Nombres Flottants, Rounding-off Errors, Erreurs d'arrondi.
Les lois de la Physique classique sont indépendantes du sens de l'écoulement du temps.
Prenons un exemple simple en utilisant un mobile P de coordonnée X et de vitesse V sur une droite D et examinons son
déplacement :
T=0 : X0
T=dT : X1 = X0 + V.dT
et à cet instant, inversons la vitesse V :
T=2.dT : X2 = X1 - V.dT = (X0 + V.dT) - V.dT = X0
Ainsi, le point P est revenu à sa position de départ...
Les grandeurs Xi, V et dT sont des nombres réels [01].
Evidemment, les systèmes étudiés, en Physique en particulier, sont beaucoup beaucoup plus complexes que l'exemple naïf présenté ci-dessus.
et en général il est nécessaire de faire appel à l'ordinateur pour les étudier.
Or, malheureusement les nombres réels n'existent pas dans l'univers fini du numérique ce qui implique
d'inévitables erreurs d'arrondi !
Et du coup, qu'en est-il de la réversibilité du temps "numérique" ?
Pour répondre à cette question, prenons l'exemple du billard bidimensionnel [02]. Utilisons donc un domaine rectangulaire plan
à l'intérieur duquel nous disposons régulièrement sur un réseau carré N boules de mêmes masses et
immobiles sauf une dont la vitesse est non nulle et aléatoire -au milieu et à droite- [03].
Au cours du temps, les particules se heurtent et les chocs sont parfaitement élastiques : il y a conservation de la quantité de mouvement.
Au milieu temporel de cette simulation toutes les vitesses sont inversées [04]. En théorie, cela signifie que toutes les boules
vont revenir à leur position de départ. Mais cela reste-t-il vrai dans un ordinateur ?
:
Avec peu de particules (N=192) l'état final est identique à l'état initial. Les erreurs d'arrondi sont peu nombreuses
et le processus est numériquement réversible.
:
Avec plus de particules (N=336) l'état final n'est plus identique à l'état initial. Les erreurs d'arrondi sont suffisamment
nombreuses pour que les particules ne reviennent pas à leur point de depart : le processus est numériquement irréversible.
:
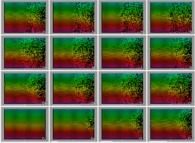Avec beaucoup plus de particules (N=768 et N=1376) le phénomène d'irréversibilité numérique ne peut que s'aggraver !
On observe donc une sorte d'effet de seuil : réversibilité avec peu de particules et irréversibilité lorsqu'elles sont plus nombreuses.
En conclusion et en toute généralité le temps n'est pas réversible dans nos ordinateurs, alors que la Physique sous-jacente l'est...
- [01]
Rappelons que les nombres réels sont les nombres de la Physique.
- [02]
On trouvera dans cette galerie de nombreux exemples de billards bidimensionnels.
- [03]
La couleur de chaque boule est fonction de ses coordonnées initiales {X0,Y0}.
- [04]
Ce qui signifie que pour chaque vecteur vitesse {Vx,Vy} est remplacé par {-Vx,-Vy}
au même instant.
Copyright © Jean-François COLONNA, 2025-2025.
Copyright © CMAP (Centre de Mathématiques APpliquées) UMR CNRS 7641 / École polytechnique, Institut Polytechnique de Paris, 2025-2025.
